
【题目】已知:如图,BE∥CF,且BE=CF,若BE、CF分别平分∠ABC和∠BCD.
(1)请判断AB与CD是否平行?并说明你的理由.
(2)CE、BF相等吗?为什么?

科目:初中数学 来源: 题型:
【题目】如图,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,∠A=∠B=30°.
(1)求证:BD是⊙O的切线;
(2)若点N在⊙O上,且DN⊥AB,垂足为M,NC=10,求AD的长.
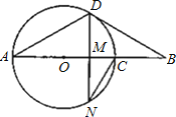
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“数学小论文”评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为l:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有____篇.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)16÷(﹣![]() )﹣3﹣(﹣
)﹣3﹣(﹣![]() )×(﹣4)
)×(﹣4)
(2)2(a2b+ab2)﹣2(a2b﹣1)﹣ab2+2
(3)(a﹣b﹣2)(a﹣b+2)
(4)899×901+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
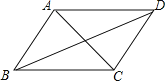
A. AB//CD, AD=BCB. ∠B=∠C,∠A=∠D
C. AB=AD, BC=CDD. AB=CD, AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的3倍,则称这样的方程为“立根方程”.以下关于立根方程的说法:
①方程x2﹣4x﹣12=0是立根方程;
②若点(p,q)在反比例函数y=![]() 的图象上,则关于x的方程px2+4x+q=0是立根方程;
的图象上,则关于x的方程px2+4x+q=0是立根方程;
③若一元二次方程ax2+bx+c=0是立根方程,且相异两点M(1+t,s),N(4﹣t,s)都在抛物线y=ax2+bx+c上,则方程ax2+bx+c=0的其中一个根是![]() .
.
正确的是( )
A. ①② B. ② C. ③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(﹣2010)0+![]() ﹣2sin60°﹣3tan30°+
﹣2sin60°﹣3tan30°+![]() ;
;
(2)解方程:x2﹣6x+2=0;
(3)已知关于x的一元二次方程x2﹣mx﹣2=0.
①若﹣1是方程的一个根,求m的值和方程的另一根;
②证明:对于任意实数m,函数y=x2﹣mx﹣2的图象与x轴总有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点D3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形AnBnCnDn的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-2,0),顶点坐标为(2,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①当x>6时,y<0;②5a+b>0;③![]() ≤a≤-
≤a≤-![]() ,④4≤n<5中,正确有( )
,④4≤n<5中,正确有( )
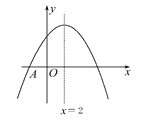
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com