
【题目】我们定义:从三角形一个顶点引出一条射线与对边相交,如果顶点与交点之间的线段把这个三角形分割成两个小的等腰三角形,那么我们就说原三角形为“可分割三角形”,这条线段叫做这个三角形的分割线.
(1)已知![]() ,
,![]() ,
,![]() ,则
,则![]() 可分割三角形.(填“是”或“不是”)
可分割三角形.(填“是”或“不是”)
(2)小愿研究发现,下图的两个三角形都是可分割三角形,请你画出每个三角形的分割线,并标出分成的等腰三角形顶角的度数.


(3)若![]() 是可分割三角形,
是可分割三角形,![]() ,
,![]() 为钝角,请通过画图的方式写出
为钝角,请通过画图的方式写出![]() 所有可能的度数(画出图形,标示
所有可能的度数(画出图形,标示![]() 的度数).
的度数).
【答案】(1)是;(2)见解析;(3)见解析,![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据等腰三角形的性质作图求出各角度即可证明;
(2)根据可分割三角形的定义即可作图求解;
(3)根据题意分情况讨论作图即可求解.
解:(1)∵在![]() 中
中![]() ,
,![]() ,
,
∴∠ABC=∠C=72°,
如图,作BD=BC,
∴∠BDC=72°,∠DBC=36°,
∴∠ABD=∠ABC-∠DBC=36°,
∴△ABD与△BDC都是等腰三角形,
则![]() 是可分割三角形.
是可分割三角形.

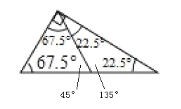
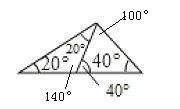
(2)如图,过直角顶点作一条直线,将直角三角形分成两个小等腰三角形,它们的顶角分别为45°和135°;过钝角顶点作一条直线,将钝角三角形分成两个小等腰三角形,它们的顶角分别为100°和140°;
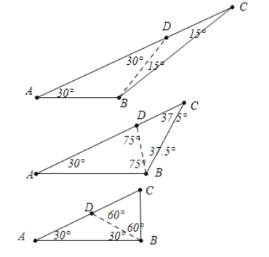
(3)如图中,当![]() 是特异线时,如果
是特异线时,如果![]() ,
,
则![]() ,
,
如果![]() ,
,![]() ,
,
则![]() ,
,
如果![]() ,
,![]() ,
,
则![]() (不合题意舍去),
(不合题意舍去),
如图中,当![]() 是特异线时,
是特异线时,![]() ,
,![]() ,则
,则![]() ,
,
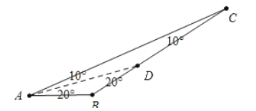
![]() 符合条件的
符合条件的![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() .
.
如果![]() ,
,![]() ,
,
则![]()
![]()
![]()
如果![]() ,
,![]() ,
,
则![]()
![]()
![]() (不合题意舍弃)
(不合题意舍弃)
如图中,当![]() 是特异线时,
是特异线时,![]() ,
,![]() ,
,
则![]()

当![]() 为特异线时,不合题意.
为特异线时,不合题意.
![]() 符合条件的
符合条件的![]() 的度数为
的度数为![]() 或
或![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】八年级的小明同学通到这样一道数学题目:△ABC为边长为4的等边三角形,E是边AB边上任意一动点,点D在CB的延长线上,且满足AE=BD.

(1)如图①,当点E为AB的中点时,DE= ;
(2)如图②,点E在运动过程中,DE与EC满足什么数量关系?请说明理由;
(3)如图③,F是AC的中点,连接EF.在AB边上是否存在点E,使得DE+EF值最小?若存在,求出这个最小值;若不存在,请说明理由.(直角三角形中,30°所对的边是斜边的一半)
查看答案和解析>>
科目:初中数学 来源: 题型:
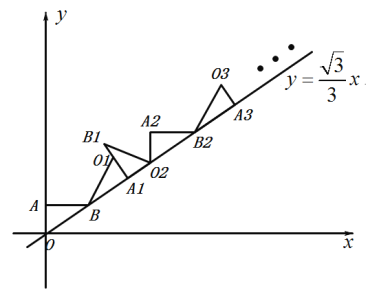
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,使点
的位置,使点![]() 对应点
对应点![]() 落在直线
落在直线![]() 上,再将
上,再将![]() 绕点
绕点![]() 旋转到
旋转到![]() 的位置,使点
的位置,使点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上,依次进行下去…,若点
上,依次进行下去…,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的横坐标为___________.
的横坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
![]() 利用图中条件,求
利用图中条件,求![]() 的值并求出反比例函数和一次函数的解析式;
的值并求出反比例函数和一次函数的解析式;
![]() 根据图象直接写出
根据图象直接写出![]() 时
时![]() 的取值范围;
的取值范围;
![]() 求
求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小儿是同班同学,被分到了同一个学习小组,在一次数学活动课上,他们各自用一张面积为![]() 的正方形纸片制作了一副七巧板,合作完成了如图所示的作品.请计算图中打圈部分的面积是( )
的正方形纸片制作了一副七巧板,合作完成了如图所示的作品.请计算图中打圈部分的面积是( )
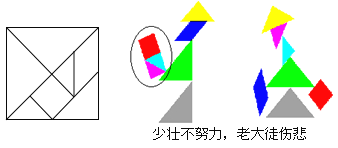
少壮不努力,老大徒伤悲
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某直销公司现有![]() 名推销员,
名推销员,![]() 月份每个人完成销售额(单位:万元),数据如下:
月份每个人完成销售额(单位:万元),数据如下:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
整理上面的数据得到如下统计表:
销售额 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)统计表中的![]() ;
;![]() ;
;
(2)销售额的平均数是 ;众数是 ;中位数是 .
(3)![]() 月起,公司为了提高推销员的积极性,将采取绩效工资制度:规定一个基本销售额,在基本销售额内,按
月起,公司为了提高推销员的积极性,将采取绩效工资制度:规定一个基本销售额,在基本销售额内,按![]() 抽成;从公司低成本与员工愿意接受两个层面考虑,你认为基本销售额定位多少万元?请说明理由.
抽成;从公司低成本与员工愿意接受两个层面考虑,你认为基本销售额定位多少万元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F ,且DC=FC,点D的坐标为(12,-2).
(1)判断⊙P与x轴的位置关系,并说明理由;
(2)求⊙P半径;
(3)若弧BD上有一动点M,连接AM,过B点作BN⊥AM,垂足为N,连DN,则DN的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I是ABC的内心,AI向延长线和△ABC的外接圆相交于点D,连接BI,BD,DC下列说法中错误的一项是( )
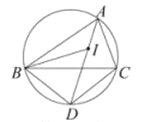
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI熏合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com