
 如图所示,在⊙O中,
如图所示,在⊙O中, |
| AD |
 |
| AC |
 |
| AD |
 |
| AC |
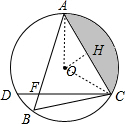 (2)过O作OH⊥AC于H,连接OA、OC,
(2)过O作OH⊥AC于H,连接OA、OC,| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 120 |
| 360 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
| y |
| x |
| 5 |
| 6 |
| x |
| y |
| 5 |
| 6 |
| x |
| 6 |
| y |
| 5 |
| 5 |
| x |
| y |
| 6 |
| A、①③ | B、②③ | C、②④ | D、③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
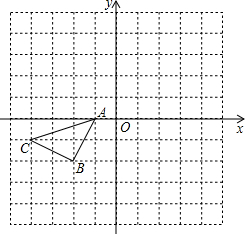 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2.5cm或6.5cm |
| B、2.5cm |
| C、6.5cm |
| D、5cm或13cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
 长城家俱雪松路分店为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小强为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°.
长城家俱雪松路分店为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小强为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com