
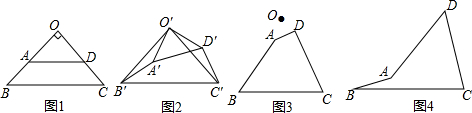
���� ��1�������ȸ���AD��BC���ɵ�$\frac{OA}{OB}=\frac{OD}{OC}$���ݴ��Ƶ�OA=OD��O��A��=O��D�䣻Ȼ���Ƶ�O��B��=O��C�䣬��A��O��B��=��D��O��C��=���㣬����ȫ���������ж��ķ����������Ƶá�O��A��B��ա�O��D��C�䣮
�����ȸ��ݡ�O��A��B��ա�O��D��C�䣬�Ƶ�S��O��A��B��=S��O��D��C����Ȼ�����S�ı���A��B��C��D��=S��O��B��C��+S��O��D��C��-S��O��A��B��-S��O��A��D�����Ƶ�S�ı���A��B��C��D��=S�ı���ABCD���ɣ�
��2����������OA��OB��OC��OD������ȱ�������OBC�͵ȱ�������OAD��Ȼ���õȱ�������OBC�������ȥ�ȱ�������OAD�����������ı���ABCD��������ɣ�
��3����������OA��OB��OC��OD������$\frac{OA}{OB}=\frac{OD}{OC}=\frac{AD}{BC}=\frac{3\sqrt{5}}{4\sqrt{5}}=\frac{3}{4}$���жϳ�OA=$\frac{3}{4}OB$��OD=$\frac{3}{4}$OC��Ȼ����ֱ��������OBC�������ȥֱ��������OAD�����������ı���ABCD��������ɣ�
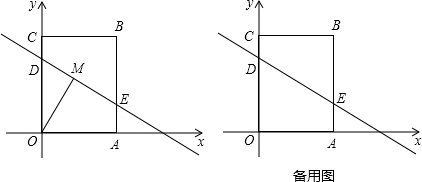
��� ��1����֤������ͼ2��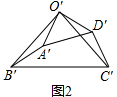
��AD��BC��
��$\frac{OA}{OB}=\frac{OD}{OC}$��
��OB=OC��
��OA=OD��
��O��A��=O��D�䣬
��OB=OC��
��O��B��=O��C�䣬
��A��O��B��=��D��O��C��=���㣬
�ڡ�O��A��B��͡�O��D��C���У�
$\left\{\begin{array}{l}{O��A��=O��D��}\\{��A��O��B��=��D��O��C��}\\{O��B��=O��C��}\end{array}\right.$��
���O��A��B��ա�O��D��C��q
�ڽ⣺�ߡ�O��A��B��ա�O��D��C�䣬
��S��O��A��B��=S��O��D��C����
��S�ı���A��B��C��D��=S��O��B��C��+S��O��D��C��-S��O��A��B��-S��O��A��D��
=��S��O��B��C��-S��O��A��D����+��S��O��D��C��-S��O��A��B����
=S��OBC-S��OAD
=S�ı���ABCD
��S�ı���A��B��C��D��=S�ı���ABCD��
��2���⣺��ͼ3������OA��OB��OC��OD��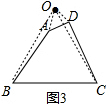 ��
��
��OA=OD��OB=OC��
��OA=OD����AOD=60�㣬
��OA=OD=AD=2��
��OB=OC����BOC=60�㣬
��OB=OC=BC=8��
��S�ı���ABCD=S��OBC-SOAD=$\frac{\sqrt{3}}{4}$����82-22��=$\frac{\sqrt{3}}{4}$��60=15$\sqrt{3}$��
��3���⣺��ͼ4������OA��OB��OC��OD��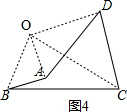 ��
��
��$\frac{OA}{OB}=\frac{OD}{OC}=\frac{AD}{BC}=\frac{3\sqrt{5}}{4\sqrt{5}}=\frac{3}{4}$��
��OA=$\frac{3}{4}OB$��OD=$\frac{3}{4}$OC��
�ߡ�BOC=90�㣬BC=4$\sqrt{5}$��
����0B=4��OC=8��
��OA=$\frac{3}{4}OB$=$\frac{3}{4}��4=3$��OD=$\frac{3}{4}$OC=$\frac{3}{4}��8$=6��
��S�ı���ABCD=S��OBC-SOAD=4��8��2-3��6��2=16-9=7��
���� ��1��������Ҫ�����˼��α任�ۺ��⣬�����˷����������������������ν��˼���Ӧ�ã������˿ռ�����������Ӧ�ã�Ҫ�������գ�
��2�����������ȫ�������ε��ж������ʵ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ�����ж�����1��SSS--�����߷ֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����2��SAS--������нǷֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����3��ASA--���Ǽ���б߷ֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����4��AAS--���Ǽ�����һ���ǵĶԱ߶�Ӧ��ȵ�����������ȫ�ȣ����ж�����5��HL--б����ֱ�DZ߶�Ӧ��ȵ�����ֱ��������ȫ�ȣ�
��3��������������������ε��ж������ʵ�Ӧ�ã��Լ�ֱ�������ε����ʵ�Ӧ�ã�Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5$\sqrt{2}$ | B�� | 3$\sqrt{5}$-6 | C�� | 3$\sqrt{6}$-5 | D�� | 2$\sqrt{10}$-6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
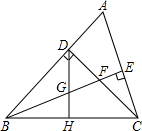 ��֪����ͼ����ABC�У���ABC=45�㣬CD��AB��D��BEƽ�֡�ABC����BE��AC��E����CD�ཻ�ڵ�F��H��BC�ߵ��е㣬����DH��BE�ཻ�ڵ�G��
��֪����ͼ����ABC�У���ABC=45�㣬CD��AB��D��BEƽ�֡�ABC����BE��AC��E����CD�ཻ�ڵ�F��H��BC�ߵ��е㣬����DH��BE�ཻ�ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��2�� | B�� | ��1��3�� | C�� | ��2��3�� | D�� | ��2��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��9�� | B�� | ��6��1�� | C�� | ��-1��8�� | D�� | ��7��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com