
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
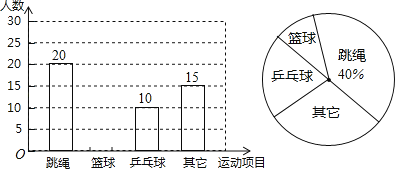
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 .
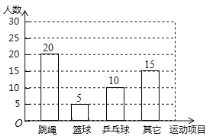
(2)请将条形统计图补充完整.
(3)如果学校有800名学生,估计全校学生中有多少人喜欢篮球项目.
【答案】(1)5,20%;(2)补全图形见解析;(3)80人
【解析】
(1)先利用跳绳的人数和它所占的百分比计算出调查的总人数,再用总人数分别减去喜欢其它项目的人数可得到喜欢篮球项目的人数,再计算出喜欢乒乓球项目的百分比,然后用800乘以样本中喜欢篮球项目的百分比可估计全校学生中喜欢篮球项目的人数;
(2)根据(1)求出的篮球的人数,即可作出;
(3)用800乘以样本中喜欢篮球的比例即可.
解:(1)调查的总人数为:20÷40%=50(人),
所以喜欢篮的人数有:50﹣20﹣10﹣15=5(人),
“乒乓球”的百分比=![]() =20%;
=20%;
故答案为:5,20%;
(2)根据(1)求出的篮球的人数,补全统计图如下:
(3)根据题意得:800×![]() =80(人),
=80(人),
答:估计全校学生中有80人喜欢篮球项目.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将两条邻边长分别为![]() ,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的_____(填序号).
,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的_____(填序号).
①![]() ,②1,③
,②1,③![]() ﹣1,④
﹣1,④![]() ,⑤
,⑤![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
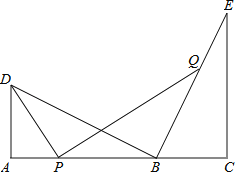
【题目】如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;
(i)当点P与A,B两点不重合时,求![]() 的值;
的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
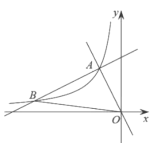
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数![]() 、
、![]() 的图象交于B、A两点,则∠OAB大小的变化趋势为( )
的图象交于B、A两点,则∠OAB大小的变化趋势为( )
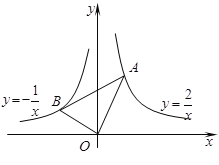
A.逐渐变小B.逐渐变大C.时大时小D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区游泳馆夏季推出两种收费方式.方式一:先购买会员证,会员证200元,只限本人当年使用,凭证游泳每次需另付费10元:方式二:不购买会员证,每次游泳需付费20元.
(1)若甲计划今年夏季游泳的费用为500元,则选择哪种付费方式游泳次数比较多?
(2)若乙计划今年夏季游泳的次数超过15次,则选择哪种付费方式游泳花费比较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
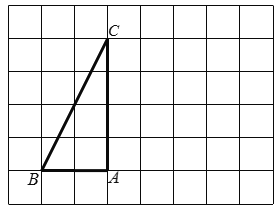
【题目】如图,在每个小正方形的边长为![]() 的网格中,△
的网格中,△![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上.
均在格点上.
(1)![]() 的长等于_____________;
的长等于_____________;
(2)在如图所示的网格中,将△![]() 绕点
绕点![]() 旋转,使得点
旋转,使得点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,得到△
上,得到△![]() ,请用无刻度的直尺,画出△
,请用无刻度的直尺,画出△![]() ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+c+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①抛物线的对称轴是直线x=1;
②若OC=OB,则c=2;
③若M(x0,y0)是x轴上方抛物线上一点,则(x0﹣a)(x0﹣b)<0;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2.其中真命题个数是( )
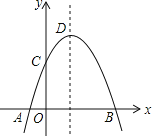
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com