
 如图,正方形ABCD的边长为4,点P,Q,R,S分别在AB,BC,CD,DA上,且BQ=2AP,CR=3AP,DS=4AP.
如图,正方形ABCD的边长为4,点P,Q,R,S分别在AB,BC,CD,DA上,且BQ=2AP,CR=3AP,DS=4AP.| AP |
| BQ |
| AS |
| BP |
| 4-4x |
| 4-x |
| 1 |
| 2 |
| AP |
| BQ |
| AS |
| BP |
| AS |
| PB |
| 1 |
| 2 |
| 4-4x |
| 4-x |
| 1 |
| 2 |
| 4 |
| 7 |
| 4 |
| 7 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 |
| 23 |
| 3 |
| 5 |
| 6 |
| 5 |
| 6 |
| 23 |
| 3 |


科目:初中数学 来源: 题型:
A、2.8×(1-
| ||
B、2.8×(1-
| ||
C、2.8÷(1+
| ||
D、2.8÷(1+
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角三角形ABC纸片上剪出如图所示的正方体的展开图,直角三角形的两直角边与正方体展开图左下角正方形的边重合,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图中正方形的边长是
如图,在直角三角形ABC纸片上剪出如图所示的正方体的展开图,直角三角形的两直角边与正方体展开图左下角正方形的边重合,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图中正方形的边长是查看答案和解析>>
科目:初中数学 来源: 题型:
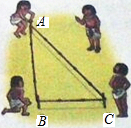 相传,古埃及人用13个等距的结把一根绳子分成等长的12段.并把它摆成△ABC的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,并说明理由.
相传,古埃及人用13个等距的结把一根绳子分成等长的12段.并把它摆成△ABC的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小明和小刚的家分别在A﹑B两地,ON是去往学校的马路,他们每次上学时都约在ON上一点C,这一点与他们家的距离分别相等.请用尺规作图的方法在图中作出点C(保留作图痕迹).
如图,小明和小刚的家分别在A﹑B两地,ON是去往学校的马路,他们每次上学时都约在ON上一点C,这一点与他们家的距离分别相等.请用尺规作图的方法在图中作出点C(保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:
1+
|
1+
|
1+
|
1+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com