
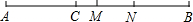 如图,线段AB的长为8cm,C是线段AB上的一点,AC=3.2cm,M是AB的中点,N是CB的中点.
如图,线段AB的长为8cm,C是线段AB上的一点,AC=3.2cm,M是AB的中点,N是CB的中点.分析 (1)根据M是AB的中点,求出BM,再根据N是BC的中点求出NB的长度,再利用MN=BM-BN即可求出MN的长度;
(2)要进行分类讨论,点C在A的两侧解法不同.
解答 解:(1)∵由AB=8,M是AB的中点,
∴AM=BM=4,
又∵AC=3.2,
∴CB=AB-AC=8-3.2=4.8(cm).
∵N是BC的中点,
∴NB=2.4,
∴MN=BM-BN=4-2.4=1.6(cm).
故答案为1.6cm.
(2)①当点C在线段AB上时,结果如(1);
②当点C在线段BA的延长线上时,
CB=AB+AC=8+3.2=11.2(cm),
∵AB=8,M是AB的中点,
∴AM=BM=4,
∵N是BC的中点,
∴NB=5.6,
∴MN=BN-BM=5.6-4=1.6(cm),
综上可知,MN=1.6cm,
故答案为1.6cm.
点评 本题前两问主要根据题中图形得到各线段之间的关系,求出MN的长度,而第三问要分情况讨论,M在AB不同侧时有不同的情况,分析各情况得到MN的表达式.


科目:初中数学 来源: 题型:解答题
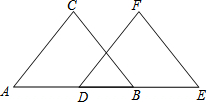 已知:如图,BC∥EF,AD=BE,BC=EF
已知:如图,BC∥EF,AD=BE,BC=EF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现有一块长40cm,宽20cm的长方形铁皮,在它的四个角分别剪去一个大小完全相同的小正方形,用剩余的部分做成一个底面积为300cm2的无盖长方体盒子,请求出剪去的小正方形的边长.
现有一块长40cm,宽20cm的长方形铁皮,在它的四个角分别剪去一个大小完全相同的小正方形,用剩余的部分做成一个底面积为300cm2的无盖长方体盒子,请求出剪去的小正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
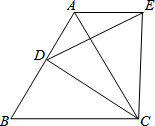 如图,点D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,请探究在点D的运动过程中,∠DAE的度数是否会发生变化?如果发生变化,请说明理由;如果不发生变化,请求出这个度数.
如图,点D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,请探究在点D的运动过程中,∠DAE的度数是否会发生变化?如果发生变化,请说明理由;如果不发生变化,请求出这个度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
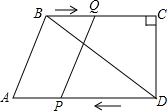 如图,在四边形ABCD中,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,同时动点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,当点P运动到与点A重合时,点Q随之停止.设运动时间为t(秒).
如图,在四边形ABCD中,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,同时动点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,当点P运动到与点A重合时,点Q随之停止.设运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
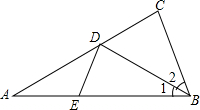 如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB=( )
如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB=( )| A. | 36° | B. | 54° | C. | 60° | D. | 72° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com