
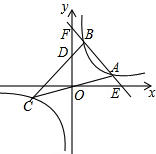
 已知:一次函数y=-2x+10的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象相交于A,B两点(A在B的右侧).直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.$\frac{BC}{BD}$=$\frac{5}{2}$,△ABC的面积=10.
已知:一次函数y=-2x+10的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象相交于A,B两点(A在B的右侧).直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.$\frac{BC}{BD}$=$\frac{5}{2}$,△ABC的面积=10. 分析 过点B作BM⊥y轴于M,过点C作CN⊥y轴于N,连接AD,如图,由$\frac{{S}_{△ABD}}{{S}_{△ABC}}$=$\frac{BD}{BC}$=$\frac{2}{5}$可知,要求△ABC的面积,只需求△ABD的面积,只需求出点A、B、D、F的坐标.易得$\frac{BM}{CN}$=$\frac{2}{3}$,可设BM=2x,就用含有x和k的代数式表示点A、B的坐标,然后代入直线y=-2x+10就可解决问题.
解答 解:过点B作BM⊥y轴于M,过点C作CN⊥y轴于N,连接AD,如图,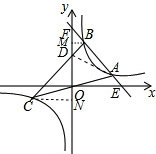 则有BM∥CN,
则有BM∥CN,
∴△BMD∽△CND,
∴$\frac{BM}{CN}$=$\frac{BD}{CD}$.
∵$\frac{BC}{BD}$=$\frac{5}{2}$,
∴$\frac{BM}{CN}$=$\frac{BD}{CD}$=$\frac{2}{3}$.
设BM=2x,则CN=3x,
∴点B(2x,$\frac{k}{2x}$),点C(-3x,-$\frac{k}{3x}$).
根据对称性可得点A(3x,$\frac{k}{3x}$).
∵点A、B在直线y=-2x+10上,
∴$\left\{\begin{array}{l}{\frac{k}{3x}=-2×3x+10}\\{\frac{k}{2x}=-2×2x+10}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{k=12}\end{array}\right.$,
∴点A(3,4),点B(2,6),点C(-3,-4).
设直线BC的解析式为y=mx+n,
则有$\left\{\begin{array}{l}{2m+n=6}\\{-3m+n=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=2}\\{n=2}\end{array}\right.$,
∴直线BC的解析式为y=2x+2.
∵点D是直线BC与y轴的交点,
∴点D(0,2).
∵点F是直线AB与y轴的交点,
∴点F(0,10),
∴S△ABD=S△ADF-S△BDF
=$\frac{1}{2}$×(10-2)×3-$\frac{1}{2}$×(10-2)×2=4.
∵$\frac{{S}_{△ABD}}{{S}_{△ABC}}$=$\frac{BD}{BC}$=$\frac{2}{5}$,
∴S△ABC=$\frac{5}{2}$S△ABD=$\frac{5}{2}$×4=10.
故答案为10.
点评 本题主要考查了一次函数与反比例函数的图象的交点、运用待定系数法求一次函数的解析式、相似三角形的判定与性质、直线上点的坐标特征、等高三角形的面积比等于底的比等知识,用含有x和k的代数式表示点A、B的坐标,代入直线y=-2x+10求出A、B的坐标,是解决本题的关键.


科目:初中数学 来源: 题型:解答题
 正方形ABCD,点E在AD上,点F为CE的中点,过点F作CE的垂线交AB,CD于点H,G.
正方形ABCD,点E在AD上,点F为CE的中点,过点F作CE的垂线交AB,CD于点H,G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
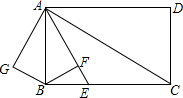 如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.
如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解电影《寻龙诀》在我市中学生中的口碑适合全面普查方式收集数据 | |
| B. | 若甲队成绩的方差是2,乙队成绩的方差是3,说明甲队成绩比乙队成绩稳定 | |
| C. | 一组数据4,6,7,6,7,8,9,中位数和众数都是6 | |
| D. | 明天下雨的概率为1%,所以明天一定不下雨 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
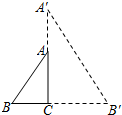 如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=$\frac{3}{5}$,现作如下操作:将△ACB沿直线AC翻折,然后再放大得到△A′CB′,联结A′B,如果△AA′B是等腰三角形,那么B′C的长是$\frac{27}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=$\frac{3}{5}$,现作如下操作:将△ACB沿直线AC翻折,然后再放大得到△A′CB′,联结A′B,如果△AA′B是等腰三角形,那么B′C的长是$\frac{27}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com