
【题目】如图,矩形ABCD中,AD=20,AB=32,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点F落在矩形ABCD的对称轴上时,则DE的长为_____
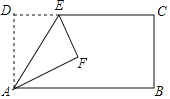
【答案】10或![]() .
.
【解析】
过点F作MN⊥AB于点N,MN交CD于点M,如图,由矩形有两条对称轴可知要分两种情况考虑,根据折叠的特性可找出各边的关系,然后在Rt△AFN与Rt△EMF中,利用勾股定理得出关于DE长度的方程,解方程即可得出结果.
解:过点F作MN⊥AB于点N,MN交CD于点M,如图所示.
设DE=a,则EF=a.
∵矩形![]() 有两条对称轴,∴分两种情况考虑:
有两条对称轴,∴分两种情况考虑:
①当DM=CM时,AN=DM=![]() CD=
CD=![]() AB=16,AD=AF=20,
AB=16,AD=AF=20,
在Rt△AFN中,由勾股定理可知:NF=![]() =12,
=12,
∴MF=MN﹣NF=AD﹣NF=8,EM=DM﹣DE=16﹣a,
∵EF2=EM2+MF2,即a2=(16﹣a)2+64,
解得:a=10;
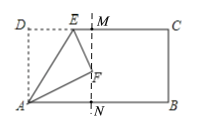
②当MF=NF时,MF=NF=![]() MN=
MN=![]() AD=10,
AD=10,
在Rt△AFN中,由勾股定理可知:AN=![]() =10
=10![]() ,
,
∴EM=DM﹣DE=AN﹣DE=10![]() ﹣a,
﹣a,
∵EF2=EM2+MF2,即a2=(10![]() ﹣a)2+102,
﹣a)2+102,
解得:a=![]() .
.
综上知:DE=10或![]() .
.
故答案为:10或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=12,AM,BN是⊙O的两条切线,DC切⊙O于E,交BN于C,设AD=x,BC=y.
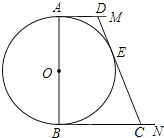
(1)求y与x的函数关系式;
(2)若x,y是2t2-30t+m=0的两实根,求x,y的值;
(3)求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.
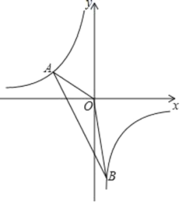
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为![]() ,顶点距水面
,顶点距水面![]() ,小孔顶点距水面
,小孔顶点距水面![]() .当水位上涨刚好淹没小孔时,大孔的水面宽度为________
.当水位上涨刚好淹没小孔时,大孔的水面宽度为________![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
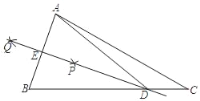
【题目】如图,在锐角△ABC中,小明进行了如下的尺规作图:
①分别以点A、B为圆心,以大于![]() AB的长为半径作弧,两弧分别相交于点P、Q;
AB的长为半径作弧,两弧分别相交于点P、Q;
②作直线PQ分别交边AB、BC于点E、D.
(1)小明所求作的直线DE是线段AB的 ;
(2)联结AD,AD=7,sin∠DAC=![]() ,BC=9,求AC的长.
,BC=9,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com