
如图2 - 50所示,抛物线y=-(x+1)2+m(x+1)(m为常数)与x轴交于A,B两点,与y轴交于点C,顶点M在第一象限,△AOC的面积为1.5,点D是线段AM上一个动点,在矩形DEFG中,点G,F在x轴上,点E在MB上.
(1)求抛物线的解析式;
(2)当DE=1时,求矩形DEFG的面积;
(3)矩形DEFG的面积是否存在最大值?如果存在,请求出这个最大值,并指出此时点D的坐标;如果不存在,请说明理由.
解:(1)由y=-(x+1)2+m(x+1),得A(-1,0),C(0,m-1),则OA=l,OC =m-1.∵S△OAC=1.5,∴
=m-1.∵S△OAC=1.5,∴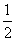 ×1×(m-1
×1×(m-1 )=1.5,∴m=4,∴y=-x2+2x+3.(2)由y=-(x-1)2+4,令y=0,得-(x-1)2+4=0,解得x1=-1,x2=3,∴A(-l,0),B(3,0),M(1,4),∴直线AM的解析式为y=2x+2.由点D在线段AM上,可设点D的坐标为(a,2a+2),-1<a<1.当DE=1时,由抛物线对称性可知1-a=0.5,∴a=0.5,2a+2=3,∴S矩形DEFG=DE·DG=1×3=3. (3)S矩形DEFG存在最大值.设D点坐标为(a,2a+2),-l<a<l,由抛物线对称性可知D
)=1.5,∴m=4,∴y=-x2+2x+3.(2)由y=-(x-1)2+4,令y=0,得-(x-1)2+4=0,解得x1=-1,x2=3,∴A(-l,0),B(3,0),M(1,4),∴直线AM的解析式为y=2x+2.由点D在线段AM上,可设点D的坐标为(a,2a+2),-1<a<1.当DE=1时,由抛物线对称性可知1-a=0.5,∴a=0.5,2a+2=3,∴S矩形DEFG=DE·DG=1×3=3. (3)S矩形DEFG存在最大值.设D点坐标为(a,2a+2),-l<a<l,由抛物线对称性可知D E=2(1-a),DG=2a+2.∴S矩形DEFG=DE·DG=2(1-a)·(2a+2)=-4a2+4,而-1<a<l,∴当a=0时,S取得最大值为4,此时D点坐标为(0,2).
E=2(1-a),DG=2a+2.∴S矩形DEFG=DE·DG=2(1-a)·(2a+2)=-4a2+4,而-1<a<l,∴当a=0时,S取得最大值为4,此时D点坐标为(0,2).


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
从总体中抽取一部分数据作为样本去估计总体的某种属性.下面叙述正确的是( )
A.样本容量越大,样本平均数就越大
B.样本容量越大,样本的方差就越大
C.样本容量越大,样本的极差就越大
D.样本容量越大,对总体的估计就越准确
查看答案和解析>>
科目:初中数学 来源: 题型:
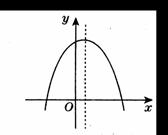
二次函数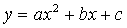 图象如图所示,则下列结论正确的( )
图象如图所示,则下列结论正确的( )
A.a>0,b<0,c>0 B.a<0,b<0,c>0
C.a<0,b>0,c<0 D.a<0,b>0,c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数的图象(0≤x≤3)如图3-4-4.关于该函数在所给自变量的取值范围内,下列说法正确的是( )
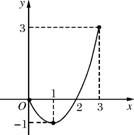
图3-4-4
A.有最小值0,有最大值3 B.有最小值-1,有最大值0
C.有最小值-1,有最大值3 D.有最小值-1,无最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如 图2 - 78所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为 ( )
图2 - 78所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为 ( )
A.1.5 m B.1.625 m C.1.66 m D.1.67 m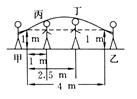
查看答案和解析>>
科目:初中数学 来源: 题型:
把8米长的钢筋,焊成一个如图4所示的框架,使其下部为矩形,上部为半圆形.请你写出钢筋所焊成框架的面积y(平方米)与半圆的半径x(米)之间的函数关系式.
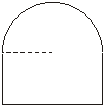
图4
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场试销一种成本为60元/件的T恤衫,规定试销期间销售单价不低于成本单价,获利不得高于成本单价的40%.经试销发现,销售量y(件)与销售单价x(元/件)符合一次函数y=kx+b,且当x=70时,y=50;当x=80时,y=40.
(1)求一次函数y=kx+b的解析式;
(2)若该商场获得的利润为w元,试写出利润w与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知⊙O的半径为8 cm,A为线段OP的中点,且OP=16 cm,则点A与⊙O的位置关系是 ( )
A.点A在⊙O内 B.点A在⊙O上
C.点A在⊙O外 D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com