
【题目】如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.

(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论.
(2)当点P移动到如图(2)的位置时,∠P与∠A、∠C又有怎样的关系?请证明你的结论.
【答案】(1) ∠APC=∠A+∠C;(2) ∠APC+∠A+∠C=360°.
【解析】
(1)过点P作PE∥AB,根据平行线的性质进行推导,即可得出∠APC=∠A+∠C;
(2)过点P作PE∥AB,根据平行线的性质进行推导,即可得出∠APC+∠A+∠C=360°.
解:(1)∠APC=∠A+∠C.理由如下:
如图1,过点P作PE∥AB,
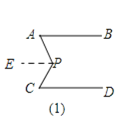
∵AB∥CD,
∴AB∥CD∥PE,
∴∠A=∠APE,∠C=∠CPE,
∴∠APC=∠APE+∠CPE=∠A+∠C.
故答案为:∠APC=∠A+∠C.
(2)∠APC+∠A+∠C=360°,理由如下:
如图2,过点P作PE∥AB,
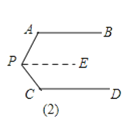
∵AB∥CD,
∴AB∥CD∥PE,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∴∠APE+∠A+∠C+∠CPE=360°;
∴∠APC+∠A+∠C=360°.
故答案为:∠APC+∠A+∠C=360°.


科目:初中数学 来源: 题型:
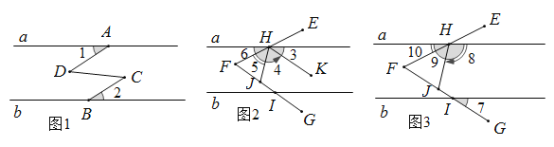
【题目】如图,A、B分别是直线a和b上的点,∠1=∠2,C、D在两条直线之间,且∠C=∠D.
(1) 证明:a∥b;
(2) 如图,∠EFG=60°,EF交a于H,FG交b于I,HK∥FG,若∠4=2∠3,判断∠5、∠6的数量关系,并说明理由;
(3) 如图∠EFG是平角的n分之1(n为大于1的整数),FE交a于H,FG交b于I.点J在FG上,连HJ.若∠8=n∠7,则∠9:∠10=______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的解析式;
(2)设P为对称轴上一动点,求△APC周长的最小值;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
分组/元 | 频 数 | 频 率 |
1000<x<1200 | 3 | 0.060 |
1200<x<1400 | 12 | 0.240 |
1400<x<1600 | 18 | 0.360 |
1600<x<1800 | a | 0.200 |
1800<x<2000 | 5 | b |
2000<x<2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布表a= ,b= ,和频数分布直方图;
(2)这50个家庭电费支出的中位数落在哪个组内?
(3)若该地区有3万个家庭,请你估计该地区有多少个一年电费支出低于1400元的家庭?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一点,且
,D是AE上的一点,且![]() ,连接BD,CD.
,连接BD,CD.

![]() 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由;
![]() 如图2,若将
如图2,若将![]() 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
![]() 如图3,若将
如图3,若将![]() 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变.
![]() 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论;
![]() 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以![]() 的AC边为直径作
的AC边为直径作![]() 交斜边AB于点E,连接EO并延长交BC的延长线于点D,作
交斜边AB于点E,连接EO并延长交BC的延长线于点D,作![]() 交BC于点F,连接EF.
交BC于点F,连接EF.
![]() 求证:
求证:![]()
![]() 求证:EF是
求证:EF是![]() 的切线;
的切线;
![]() 若
若![]() 的半径为3,
的半径为3,![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com