����⣺��1����y=2x+4�У���x=0����ã�y=4��
��B�������ǣ�0��4����
��x=1����ã�y=6��
��C�������ǣ�1��6����
�ѣ�1��6������y=
�У��ã�k=6��
��2����y=2x+4�У���y=0����ã�x=-2��
��A�������ǣ�-2��0����
��ͼ1����O��OD��AB�ڵ�D����ֱ��OD�Ľ���ʽ��y=-
x��
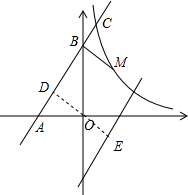
ͼ1
��������ã�
��
��ã�
��
��D�������ǣ�-
��
����D����O�ĶԳƵ���E��
��-
����
����E��ƽ����AB��ֱ�ߵĽ���ʽ�ǣ�y=2x+c����-
=
+c��
��ã�c=-4��
�����ʽ��y=2x-4��
��������ģ�
��
��ã�
��
��
��M�������ǣ�3��2����-1��-6����
��3������PBQ=90��ʱ������BP��AB��
��ͼ2������B��BP��AB����˫�����ڵ�P��
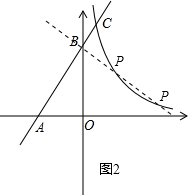
��ʱ��ֱ��AB�ϴ�������������Q�㣬
��ʱֱ��BP����Ϊ��y=-
x+4��
����˫���߷��̵ã�
��
��ã�
��
������ʱP�������Ϊ��2��3����1��6����
����BQP=90��ʱ����ͼ3����B����ֱ��BP��ʹֱ��BP��ֱ��AB�ļн�Ϊ45�㣬��˫�����ڵ�P����x���ڵ�D����ʱ��ֱ��AB�ϴ�������������Q�㣬
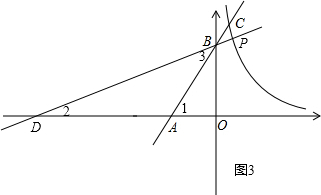
���1=��2+��3=��2+45�㣬
����tan��1=tan����2+45�㣩=
��
��tan��1=
=
=2������
=2��
���tan��1=
������ֱ��BP�ķ���Ϊ��y=
x+4��
����˫���߷��̵ã�
��
��ã�
��
����ΪP���ڵ�һ���ޣ�����ȥ����
��ʱP�������Ϊ��3
-6��
+2����
����BPQ=90��ʱ��ͬ�������P��������Ϊ��3
-6��
+2����
���Ͽ�֪����������P�������Ϊ����2��3����1��6����3
-6��
+2����







 ��֪����ͼ���ڵȱ�������ABC�У�M��N�ֱ���AB��AC���е㣬D��MN������һ�㣬CD��BD���ӳ��߷ֱ���AB��AC����F��E����
��֪����ͼ���ڵȱ�������ABC�У�M��N�ֱ���AB��AC���е㣬D��MN������һ�㣬CD��BD���ӳ��߷ֱ���AB��AC����F��E����