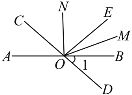
【题目】已知：如图，直线AB，CD相交于点O，∠1＝40°，∠BOE与∠BOC互补，OM平分∠BOE，且∠CON∶∠NOM＝2∶3.求∠COM和∠NOE的度数．
【答案】∠COM＝120°，∠NOE＝52°
【解析】
如图，首先根据对顶角相等可得∠6=40°，再根据同角的补角相等可得∠2+∠3=40°，根据角平分线定义可得∠2和∠3的度数，结合角的和差关系可得∠COM的度数，再利用条件∠CON：∠NOM=2：3计算出∠MON的度数，进而可得∠NOE的度数．
如图，
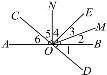
∵∠1＝40°，∴∠6＝40°.
∵∠6＋∠BOC＝180°，∠BOE与∠BOC互补，
∴∠6＝∠BOE＝40°，
∴∠BOC＝140°，
∴∠COE＝100°.
∵OM平分∠BOE，∴∠2＝∠3＝20°，
∴∠COM＝120°.
∵∠CON∶∠NOM＝2∶3，
∴∠NOM＝120°×
＝72°，
∴∠NOE＝72°－20°＝52°.
故答案为：∠COM＝120°；∠NOE＝52°.
科目：初中数学 来源： 题型：
【题目】为鼓励居民节约用水，某市决定对居民用水收费实行“阶梯价”，即当每月用水量不超过15吨时（包括15吨），采用基本价收费；当每月用水量超过15吨时，超过部分每吨采用市场价收费．小兰家4、5月份的用水量及收费情况如下表：
月份 | 用水量（吨） | 水费（元） |
4 | 22 | 51 |
5 | 20 | 45 |
（1）求该市每吨水的基本价和市场价．
（2）设每月用水量为n吨，应缴水费为m元，请写出m与n之间的函数关系式．
（3）小兰家6月份的用水量为26吨，则她家要缴水费多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
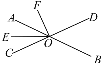
【题目】如图，直线AB，CD相交于点O，OE是∠AOC的平分线，∠BOC＝130°，∠BOF＝140°，则∠EOF的度数为( )
A. 95° B. 65°
C. 50° D. 40°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A(x，y)，点A′(x′，y′)，若x′＝x＋m，y′＝y＋n，即点A′(x＋m，y＋n)，则表示点A到点A′的一个平移．例如：点A(x，y)，点A′(x′，y′)，若x′＝x＋1，y′＝y－2，则表示点A向右平移1个单位长度，再向下平移2个单位长度得到点A′.
根据上述定义，探究下列问题：
(1)已知点A(x，y)，A′(x－3，y)，则线段AA′的长度是多少；
(2)已知点A(x，y)，A′(x＋2，y－1)，则线段AA′的长度是多少；
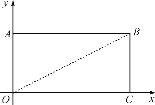
(3)长方形AOCB在平面直角坐标系中的位置如图所示，A(0，2)，C(4，0)，点A′(x′，y′)，若x′＝x＋m，y′＝y－2m(m均为正数)，点A′(x′，y′)能否在△OCB的直角边上？若能，求m的值；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】长途汽车客运公司规定旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李票费用y（元）是行李重量x（千克）的一次函数，其图象如图7所示．求出y与x之间的函数关系式，并说明行李的重量不超过多少千克，就可以免费托运？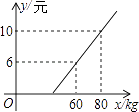
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题探索:
(1)已知一个分数
,如果分子、分母同时增加1,分数的值是增大还是减小?请说明你的理由.
(2)若正分数中分子和分母同时增加2,3,…,k(整数k>0),情况如何?
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,问:同时增加相等的窗户面积和地板面积,住宅的采光条件是变好了,还是变坏了?请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF；
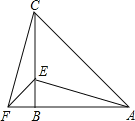
（1）求证：Rt△ABE≌Rt△CBF；
（2）求证：AB=CE+BF；
（3）若∠CAE=30°，求∠ACF度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知x、y是实数，并且 
+y2﹣6y+9=0，则（xy）2017的值是 ．
若一个等腰三角形的三边长均满足方程y2﹣6y+8=0，则此三角形的周长为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
