
【题目】已知二次函数![]() .
.
(1)该二次函数的顶点坐标为__________;
(2)该函数的图象与![]() 轴的交点坐标为__________;
轴的交点坐标为__________;
(3)用五点法画函数图象
| … | … | |||||
| … | … |
(4)当![]() 时,则
时,则![]() 的取值范围是__________;
的取值范围是__________;
(5)将该抛物线绕顶点旋转180°,所得函数的解析式为__________;
(6)抛物线![]() 与
与![]() 轴有且仅有一个交点,则
轴有且仅有一个交点,则![]() __________.
__________.

【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() (3)函数图象见解析;(4)
(3)函数图象见解析;(4)![]() ;(5)
;(5)![]() ;(6)4.
;(6)4.
【解析】
(1)将二次函数的解析式化成顶点式即可得;
(2)令![]() ,求解一元二次方程即可得;
,求解一元二次方程即可得;
(3)先列出图象上的五个点,再顺次连接即可画出函数图象;
(4)根据(3)的图象即可得;
(5)先根据旋转的性质可得顶点坐标不变,从而可得新二次函数的顶点式,再求出点![]() 绕顶点旋转
绕顶点旋转![]() 所得点的坐标,然后代入求解即可得;
所得点的坐标,然后代入求解即可得;
(6)根据二次函数![]() 的图象可知,将其向上平移4个单位长度所得的图象与
的图象可知,将其向上平移4个单位长度所得的图象与![]() 轴有且仅有一个交点,由此即可得出k的值.
轴有且仅有一个交点,由此即可得出k的值.
(1)将二次函数![]() 化成顶点式为
化成顶点式为![]()
则该二次函数的顶点坐标为![]()
故答案为:![]() ;
;
(2)令![]() 得
得![]()
解得![]()
则该函数的图象与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,![]()
故答案为:![]() ,
,![]() ;
;
(3)根据二次函数的解析式,列出五个点(注:五个点对称列出即可,不刻意要求特殊点
),如下表所示:
| … | -3 | -2 | -1 | 0 | 1 | … |
| … | 0 | -3 | -4 | -3 | 0 | … |
利用五点法画函数图象如下:
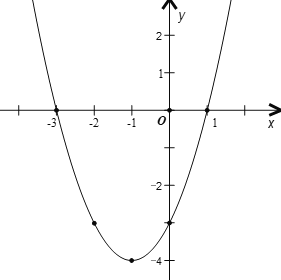
(4)由(3)所画的函数图象可知,当![]() 时,
时,![]()
故答案为:![]() ;
;
(5)如图,点B绕点A旋转![]() 的对应点为点D
的对应点为点D
由旋转的性质得:新二次函数的顶点坐标仍为![]()
设新二次函数的解析式为![]()
由点![]() 可知,
可知,![]()
由旋转的性质可知,![]()
在![]() 和
和![]() 中,
中,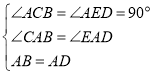
![]()
![]()
![]()
![]()
将![]() 代入
代入![]() 得,
得,![]()
解得![]()
则新二次函数的解析式为![]()
故答案为:![]() ;
;
(6)由函数图象的平移规律可知,抛物线![]() 是由二次函数
是由二次函数![]() 向上
向上![]() 或向下
或向下![]() 平移得到的
平移得到的
由二次函数![]() 的图象可知,将其向上平移4个单位长度所得的图象与
的图象可知,将其向上平移4个单位长度所得的图象与![]() 轴有且仅有一个交点
轴有且仅有一个交点
则![]()
故答案为:4.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式![]() 的实数x的所有取值的全体叫做闭区间,表示为
的实数x的所有取值的全体叫做闭区间,表示为![]() 对于一个函数,如果它的自变量x与函数值y满足:当
对于一个函数,如果它的自变量x与函数值y满足:当![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求实数a,b的值.
上的“闭函数”,求实数a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AD=3,DC=4,动点P在线段DC上以每秒1个单位的速度从点D向点C运动,过点P作PQ∥AC交AD于Q,将△PDQ沿PQ翻折得到△PQE. 设点P的运动时间为t(s).
(1)当点E落在边AB上时,t的值为 ;
(2)设△PQE与△ADC重叠部分的面积为s,求s与t的函数关系式;
(3)如图2,以PE为直径作⊙O.当⊙O与AC边相切时,求CP的长.
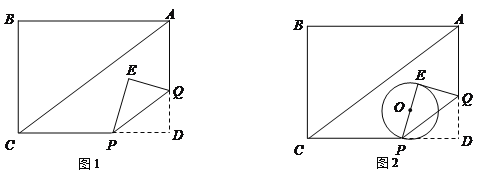
查看答案和解析>>
科目:初中数学 来源: 题型:
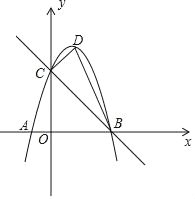
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:所有正整数在进行某种规定步骤的运算后,会得到一个恒定不变的数,我们把这个恒定不变的数叫做稳定数.规定求三位数的稳定数的运算步骤是:任意三位数A=![]() (百位与个位不相同),将这个数逆置后得A1=
(百位与个位不相同),将这个数逆置后得A1=![]() ,A与A1中较大的数减去较小的数得到一个数B,再将B进行一次逆置得B1(若B为两位数则交换十位与个位逆置),将B1与B相加得C,C就是该三位数A的稳定数,记作
,A与A1中较大的数减去较小的数得到一个数B,再将B进行一次逆置得B1(若B为两位数则交换十位与个位逆置),将B1与B相加得C,C就是该三位数A的稳定数,记作![]() .
.
材料二:当两个三位数的稳定数相同时,这两个三位数的百位数字与个位数字之差的绝对值或者都大于1,或者都等于1.
(1)求352的稳定数是 ;百位与个位相差2的三位数,它的稳定数是 .
(2)现有S=301+10p,T=100m+40+n(1≤p≤9,1≤m≤9,1≤n≤9,p,m,n均是整数),其中T是偶数,若![]() ,3p+m+n=20,|p-n|=1,
,3p+m+n=20,|p-n|=1,![]() ,请求出
,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
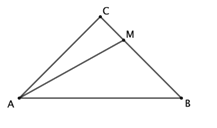
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,以点
,以点![]() 为中心,将线段
为中心,将线段![]() 顺时针旋转135°,得到线段
顺时针旋转135°,得到线段![]() ,连接
,连接![]() .
.
(1)依题意,补全图形;
(2)求证:![]() ;
;
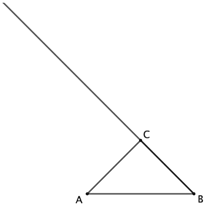
(3)点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 是点
是点![]() 关于点
关于点![]() 的对称点,写出
的对称点,写出![]() 的一个值,使得对任意的点
的一个值,使得对任意的点![]() 总有
总有![]() ,并证明.
,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过
经过![]() 点,直线
点,直线![]() 是抛物线的对称轴.
是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 的周长最小,求出点
的周长最小,求出点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上一动点,当
是抛物线上一动点,当![]() 时,请直接写出点
时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图,填表后再回答问题:
(1)在横线上填入正确的数:
![]() 的个数:8,______ ,24
的个数:8,______ ,24![]()
★的个数:1,4,______ ![]()
(2)试求第6个图形中“![]() ”的个数和“
”的个数和“![]() ”的个数?
”的个数?
(3)试求第108个图形中“![]() ”的个数与“
”的个数与“![]() ”的个数之差?
”的个数之差?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
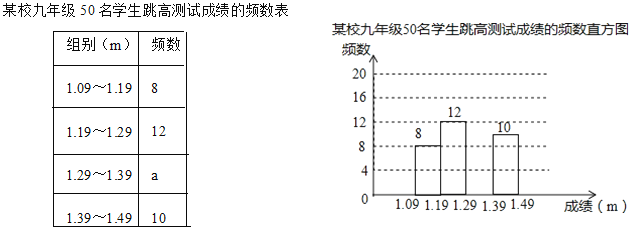
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com