练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，⊙O是以原点为圆心， 为半径的圆，点P是直线y=﹣x+6上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为______.

    【答案】4

    【解析】试题分析：由P在直线y=-x+6上，设P（m，6-m），连接OQ，OP，由PQ为圆O的切线，得到PQ⊥OQ，在直角三角形OPQ中，利勾股定理列出关系式，配方后利用二次函数的性质即可求出PQ的最小值．

    解：∵P在直线y=x+6上，

    ∴设P坐标为(m,6m)，

    连接OQ，OP，由PQ为圆O的切线，得到PQ⊥OQ，

    在Rt△OPQ中,根据勾股定理得：OP2=PQ2+OQ2，

    ∴PQ2=m2+(6m)22=2m212m+34=2(m3)2+16，

    则当m=3时，切线长PQ的最小值为4.

    故答案为：4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

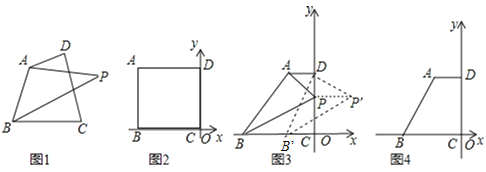
    【题目】如图1，点P为四边形ABCD所在平面上的点，如果∠PAD=∠PBC，则称点P为四边形ABCD关于A、B的等角点，以点C为坐标原点，BC所在直线为轴建立平面直角坐标系，点B的横坐标为﹣6．

    （1）如图2，若A、D两点的坐标分别为A（﹣6，4）、D（0，4），点P在DC边上，且点P为四边形ABCD关于A、B的等角点，则点P的坐标为　_________　；

    （2）如图3，若A、D两点的坐标分别为A（﹣2，4）、D（0，4）．

    ①若P在DC边上时，则四边形ABCD关于A、B的等角点P的坐标为　_________　；

    ②在①的条件下，将PB沿轴向右平移个单位长度（0＜＜6）得到线段P′B′，连接P′D，B′D，试用含的式子表示P′D2+B′D2，并求出使P′D2+B′D2取得最小值时点P′的坐标；

    ③如图4，若点P为四边形ABCD关于A、B的等角点，且点P坐标为（1， ），求的值；

    ④以四边形ABCD的一边为边画四边形，所画的四边形与四边形ABCD有公共部分，若在所画的四边形内存在一点P，使点P分别是各相邻两顶点的等角点，且四对等角都相等，请直接写出所有满足条件的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）解方程：x2-2x=4 （2）解不等式组

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上，点O为原点，点A对应的数为9，点B对应的数为b，点C在点B右侧，长度为2个单位的线段BC在数轴上移动．

    （1）当b＝5时，试求线段AC的长；

    （2）当线段BC在数轴上沿射线AO方向移动的过程中，若存在AC﹣OB＝AB，求此时满足条件的b值．

    （3）当线段BC在数轴上移动时，满足关系式|AC﹣OB|＝|AB﹣OC|，则此时的b的取值范围是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

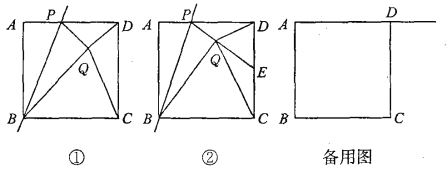
    【题目】如图①，已知正方形ABCD的边长为1，点P是AD边上的一个动点，点A关于直线BP的对称点是点Q，连接PQ、DQ、CQ、BQ，设AP＝x．

    （1）BQ＋DQ的最小值是_______，此时x的值是_______；

    （2）如图②，若PQ的延长线交CD边于点E，并且∠CQD＝90°．

    ①求证：点E是CD的中点； ②求x的值．

    （3）若点P是射线AD上的一个动点，请直接写出当△CDQ为等腰三角形时x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰△ABC的周长为21，底边BC＝5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（　　）

    A. 13B. 16C. 8D. 10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题

    某中学组织七年级师生去春游，一人一座，如果单租45座客车若干辆，则刚好坐满；如果单租60座的客车，则少租一辆，且余15个座位.

    （1）求参加春游的师生总人数.

    （2）已知一辆45座客车的租金每天250元，一辆60座客车的租金每天300元，问单租哪种客车省钱？

    （3）如果同时租用这两种客车，那么两种客车分别租多少辆最省钱？（只写出租车方案即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班“数学兴趣小组”对函数y=x2|x|的图象和性质进行了探究，探究过程如下，请补充完整：

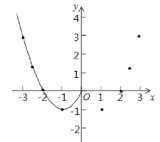
    (1)自变量x的取值范围是全体实数，x与y的几组对应值列表如下：

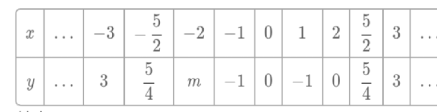
    其中，m=___.

    (2)根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分.

    (3)探究函数图象发现：

    ①函数图象与x轴有___个交点,所以对应的方程x2|x|=0有___个实数根；

    ②方程x2|x|=有___个实数根；

    ③关于x的方程x2|x|=a有4个实数根时，a的取值范围是___.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，P，Q，B在一条不完整的数轴上，点A表示数-3，点B表示数3，若动点P从点A出发以每秒1个单位长度向终点B匀速运动，同时动点Q从点B出发以每秒2个单位长度向终点A匀速运动，其中一点到达终点时，另一个点也随之停止运动，当BP=3AQ时，点P在数轴上表示的数是( )

    A.2.4B.-1.8C.0.6D.-0.6

    查看答案和解析>>

    同步练习册答案