
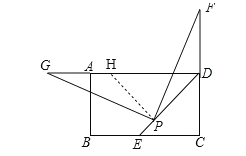
【题目】已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.
①求证:PG=PF;
②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DE、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.

【答案】(1)①证明见解析;②DG+DF=![]() DP;(2)不成立,数量关系式应为:DG﹣DF=
DP;(2)不成立,数量关系式应为:DG﹣DF=![]() DP.
DP.
【解析】
试题分析:(1)①若证PG=PF,可证△HPG≌△DPF,已知∠DPH=∠HPG,由旋转可知∠GPF=∠HPD=90°及DE平分∠ADC得△HPD为等腰直角三角形,即∠DHP=∠PDF=45°、PD=PH,即可得证;
②由△HPD为等腰直角三角形,△HPG≌△DPF知HD=![]() DP,HG=DF,根据DG+DF=DG+GH=DH即可得;
DP,HG=DF,根据DG+DF=DG+GH=DH即可得;
(2)过点P作PH⊥PD交射线DA于点H,先证△HPD为等腰直角三角形可得PH=PD,HD=![]() DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG﹣HG=DG﹣DF可得DG﹣DF=
DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG﹣HG=DG﹣DF可得DG﹣DF=![]() DP.
DP.
试题解析:(1)①∵∠GPF=∠HPD=90°,∠ADC=90°,∴∠GPH=∠FPD,∵DE平分∠ADC,∴∠PDF=∠ADP=45°,∴△HPD为等腰直角三角形,∴∠DHP=∠PDF=45°,在△HPG和△DPF中,∵∠PHG=∠PDF,PH=PD,∠GPH=∠FPD,∴△HPG≌△DPF(ASA),∴PG=PF;
②结论:DG+DF=![]() DP,由①知,△HPD为等腰直角三角形,△HPG≌△DPF,∴HD=
DP,由①知,△HPD为等腰直角三角形,△HPG≌△DPF,∴HD=![]() DP,HG=DF,∴HD=HG+DG=DF+DG,∴DG+DF=
DP,HG=DF,∴HD=HG+DG=DF+DG,∴DG+DF=![]() DP;
DP;
(2)不成立,数量关系式应为:DG﹣DF=![]() DP,如图,过点P作PH⊥PD交射线DA于点H,∵PF⊥PG,∴∠GPF=∠HPD=90°,∴∠GPH=∠FPD,∵DE平分∠ADC,且在矩形ABCD中,∠ADC=90°,∴∠HDP=∠EDC=45°,得到△HPD为等腰直角三角形,∴∠DHP=∠EDC=45°,且PH=PD,HD=
DP,如图,过点P作PH⊥PD交射线DA于点H,∵PF⊥PG,∴∠GPF=∠HPD=90°,∴∠GPH=∠FPD,∵DE平分∠ADC,且在矩形ABCD中,∠ADC=90°,∴∠HDP=∠EDC=45°,得到△HPD为等腰直角三角形,∴∠DHP=∠EDC=45°,且PH=PD,HD=![]() DP,∴∠GHP=∠FDP=180°﹣45°=135°,在△HPG和△DPF中,∵∠GPH=∠FPD,∠GHP=∠FDP,PH=PD,∴△HPG≌△DPF,∴HG=DF,∴DH=DG﹣HG=DG﹣DF,∴DG﹣DF=
DP,∴∠GHP=∠FDP=180°﹣45°=135°,在△HPG和△DPF中,∵∠GPH=∠FPD,∠GHP=∠FDP,PH=PD,∴△HPG≌△DPF,∴HG=DF,∴DH=DG﹣HG=DG﹣DF,∴DG﹣DF=![]() DP.
DP.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】将抛物线y=x2+1先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是( )
A.y=(x+2)2+2
B.y=(x+2)2﹣2
C.y=(x﹣2)2+2
D.y=(x﹣2)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )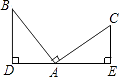
A.AD=AE
B.AB=AC
C.BD=AE
D.AD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
请根据所给信息,解答下列问题: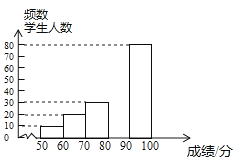
(1)a= , b=
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com