
����Ŀ����ͼ������ABCD�У�AB��CD����ABC=90����AB=8��CD=6��BC=4��AB������һ����P������A��B�غϣ�������DP����PQ��DP��ʹ��PQ���߶�BC�ڵ�E����AP=x��
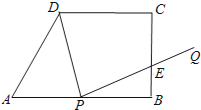
��1����xΪ��ֵʱ����APD�ǵ��������Σ�
��2������BE=y����y����x�ĺ�����ϵʽ��
��3����BC�ij�a���Ա仯�������ڵ������£��Ƿ���ڵ�P��ʹ��PQ������C���������ڣ���˵�����ɣ������ڣ�д����BC�ij���ʲô��Χ��ʱ�����Դ��������ĵ�P��ʹ��PQ������C���������Ӧ��AP�ij���
���𰸡���1����xΪ2![]() ��4��5ʱ����APD�ǵ��������Σ�
��4��5ʱ����APD�ǵ��������Σ�
��2��![]() ��
��
��3��![]()
��������
�����������1����ʾ��PH��Ȼ��֢ٵ�AP=ADʱ���ڵ�AD=PDʱ�����ݵ������������ߺ�һ�����ʣ�AH=PH����ʽ���м��㼴�ɵý⣻�۵�AP=PDʱ����ʾ��PH��Ȼ����Rt��DPH�У����ݹ��ɶ�����ʽ���м��㼴�ɵý⣻
��2������ͬ�ǵ������������HDP=��EPB���ٸ������Ƕ�Ӧ��ȣ������������������DPH����PEB���ƣ�Ȼ��������������ζ�Ӧ�߳ɱ����г�����ʽ�������ɵý⣻
��3������PQ����Cʱ��BE=4�����루2����BE�ı���ʽ���ٸ���һԪ���η��̵Ľ�ȷ�����ɣ�
�⣺��1����D����DH��AB��H�����ı���DHBCΪ���Σ�
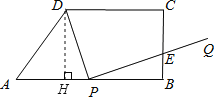
��DH=BC=4��HB=CD=6��
��AH=2��AD=2![]() ��
��
��AP=x��
��PH=x��2��
����٣���AP=ADʱ����x=2![]() ��
��
����ڣ���AD=PDʱ����AH=PH��
��2=x��2��
���x=4��
����ۣ���AP=PDʱ����Rt��DPH�У�x2=42+��x��2��2��
���x=5��
��2��x��8��
����xΪ2![]() ��4��5ʱ����APD�ǵ��������Σ�
��4��5ʱ����APD�ǵ��������Σ�
��2���ߡ�DPE=��DHP=90����
���DPH+��EPB=��DPH+��HDP=90����
���HDP=��EPB��
���ߡ�DHP=��B=90����
���DPH�ס�PEB��
��![]() ��
��
��![]() ��
��
�����ã�![]() ��
��
��3�����ڣ�
�ɣ�2������DPH�ס�PEB��
��![]() ��
��
��y=![]() ��
��
��y=aʱ����8��x����x��2��=a2����x2��10x+��16+a2��=0����=100��4��16+a2����0��
��100��64��4a2��0��
��a2��9��
����a��0��
��0��a��3��
����BC����0��BC��3ʱ�����ڵ�P��ʹ��PQ����C��
��ʱ��AP�ij�Ϊ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A(2��1)����ƽ��3����λ�õ���B�����B��������( )
A. (5��1) B. (��1��4)
C. (5��4) D. (2��4)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͼ��ʾ�Ķ��κ���y=ax2+bx+c��ͼ���У��۲�ó�������������Ϣ����1��a��O����2��b2��4ac��0����3��b��O����4��a+b+c��0����5��a��b+c��0������Ϊ������ȷ��Ϣ�ĸ����У� ��

A��2�� B��3�� C��4�� D��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A��2a2��a2=1 B����a+b��2=a2+b2
C����3b3��2=6b6 D������a��5������a��3=a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ֱ������ABCD�У�AD��BC����C=90����AB=AD=25��BC=32������BD��AE��BD����ΪE��
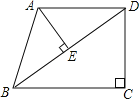
��1����֤����ABE�ס�DBC��
��2�����߶�AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֽƬ����100��������ͬ�����εĶ��㹲103�����������������㶼��������������Щ��Ϊ������������������ֽƬ����С���������������������ι���_______����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���y=x2+2x������˵����ȷ����
��ͼ������Գ�ͼ��
��ͼ�ξ����㣨��1��1��
��ͼ����һ����͵�
�ܵ�x��1ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
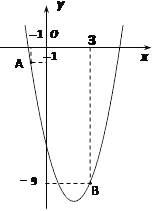
����Ŀ����ͼ����֪���κ���![]() ��ͼ����A��-1��-1���͵�B��3��-9����
��ͼ����A��-1��-1���͵�B��3��-9����
��1����ö��κ����ı���ʽ��
��2��д���������ߵĶԳ��ἰ�������ꣻ
(3)��P��m��m�����Q���ڸú���ͼ���ϣ�����m��0��������������������ߵĶԳ���Գƣ���m��ֵ����Q ��x��ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com