
| A. | $\frac{12}{5}$ | B. | $\frac{24}{5}$ | C. | 5 | D. | 6 |
分析 连接AD,根据三角形的面积公式即可得到$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=12,根据等腰三角形的性质进而求得DE+DF的值.
解答 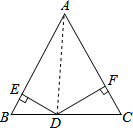 解:连接AD,∵AB=AC=5,BC=6,
解:连接AD,∵AB=AC=5,BC=6,
∵BC边上的高是4,
∴S△ABC=$\frac{1}{2}$BC×4=12,
∵S△ABD=$\frac{1}{2}$AB•DE,S△ADC=$\frac{1}{2}$AC•DF,
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=12,
∵AB=AC,
∴$\frac{1}{2}$AB(DE+DF)=12
∴DE+DF=$\frac{24}{5}$.
故选 B.
点评 本题考查了等腰三角形的性质,三角形的面积,熟记等腰三角形的性质是解题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,下面是利用尺规作∠AOB的角平分线OC的作法:
如图,下面是利用尺规作∠AOB的角平分线OC的作法:| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )| A. | 不能 | B. | 带① | C. | 带② | D. | 带③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com