
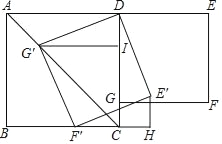
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】试题解析:作G′I⊥CD于I,G′R⊥BC于R,E′H⊥BC交BC的延长线于H.连接RF′.则四边形RCIG′是正方形.
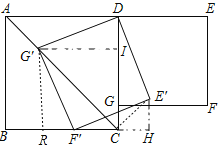
∵∠DG′F′=∠IGR=90°,∴∠DG′I=∠RG′F′,在△G′ID和△G′RF中,∵G′D= G′F,∠D G′I=∠R G′F′,G′I= G′R,∴△G′ID≌△G′RF,∴∠G′ID=∠G′RF′=90°,∴点F′在线段BC上,在Rt△E′F′H中,∵E′F′=2,∠E′F′H=30°,∴E′H=![]() E′F′=1,F′H=
E′F′=1,F′H=![]() ,易证△RG′F′≌△HF′E′,∴RF′=E′H,RG′RC=F′H,∴CH=RF′=E′H,∴CE′=
,易证△RG′F′≌△HF′E′,∴RF′=E′H,RG′RC=F′H,∴CH=RF′=E′H,∴CE′=![]() ,∵RG′=HF′=
,∵RG′=HF′=![]() ,∴CG′=
,∴CG′=![]() RG′=
RG′=![]() ,∴CE′+CG′=
,∴CE′+CG′=![]() .
.
故选A.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线型拱桥,当拱顶离水面8m时,水面宽AB为12m.当水面上升6m时达到警戒水位,此时拱桥内的水面宽度是多少m?
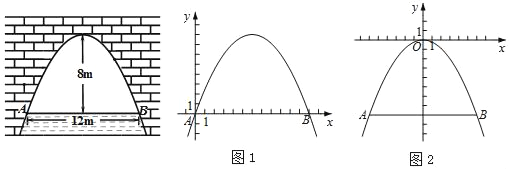
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,
此时点B的坐标为( , ),抛物线的顶点坐标为( , ),
可求这条抛物线所表示的二次函数的解析式为 .
当y=6时,求出此时自变量x的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,
这时这条抛物线所表示的二次函数的解析式为 .
当y= 时,求出此时自变量x的取值为 ,即可解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0,其中正确的命题是( )
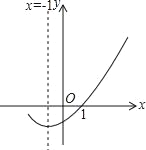
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C = 90°,∠BAC 的平分线交BC于点D,点O在AB上,以点O为圆心、OA长为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若OA = 2,∠B = 30°,求涂色部分的面积(结果保留![]() 和根号).
和根号).
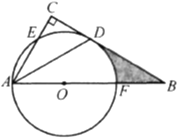
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:
例:用图象法解一元二次不等式:![]() .
.
解:设![]() ,则
,则![]() 是
是![]() 的二次函数.
的二次函数.
![]() 抛物线开口向上.
抛物线开口向上.
又![]() 当
当![]() 时,
时,![]() ,解得
,解得![]() .
.
![]() 由此得抛物线
由此得抛物线![]() 的大致图象如图所示.
的大致图象如图所示.
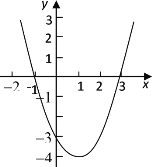
观察函数图象可知:当![]() 或
或![]() 时,
时,![]() .
.![]()
![]() 的解集是:
的解集是:![]() 或
或![]() .
.
(1)观察图象,直接写出一元二次不等式:![]() 的解集是 ;
的解集是 ;
(2)仿照上例,用图象法解一元二次不等式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在AC⊥BC,过点C的直线MN∥AB,D为AB边上一点,且AD=4,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求CE的长;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
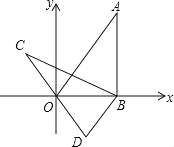
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
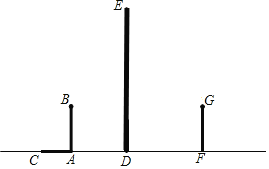
(1)请你确定灯泡所在的位置,并画出表示小亮在灯光下形成的影子线段.
(2)如果灯杆高12m,小亮的身高1.6m,小亮与灯杆的距离13m,请求出小亮影子的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com