
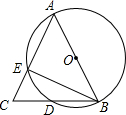
 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的个数是( )
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据圆周角定理,等边对等角,等腰三角形的性质,直径所对的圆周角是直角等知识,运用排除法逐条分析判断.
解答 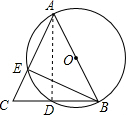 解:连接AD,AB是直径,
解:连接AD,AB是直径,
则AD⊥BC,
又∵△ABC是等腰三角形,
故点D是BC的中点,即BD=CD,故②正确;
∵AD是∠BAC的平分线,
由圆周角定理知,∠EBC=∠DAC=$\frac{1}{2}$∠BAC=22.5°,故①正确;
∵∠ABE=90°-∠EBC-∠BAD=45°=2∠CAD,故④正确;
∵∠EBC=22.5°,2EC≠BE,AE=BE,∴AE≠2CE,③不正确;
∵AE=BE,BE是直角边,BC是斜边,肯定不等,故⑤错误.
综上所述,正确的结论是:①②④.
故选B.
点评 本题考查了圆周角定理,等腰三角形的判定与性质以及弧长的计算等.利用了圆周角定理,等边对等角,等腰三角形的性质,直径所对的圆周角是直角求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 平行四边形ABCD是中心对称图形 | B. | △ABC≌△COD | ||
| C. | △AOB≌△COD | D. | △AOB与△BOC的面积相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$=$\overrightarrow{BA}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{CA}$ | C. | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | D. | $\overrightarrow{a}$+(-$\overrightarrow{a}$)=$\overrightarrow{0}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
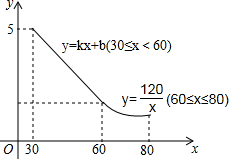 某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格x(元/个)的函数关系如图所示.
某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格x(元/个)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
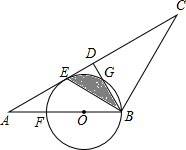 已知,如图,在△ABC中,AB=BC,D是AC的中点,BE平分∠ABD交AC于点E,点O是AB边上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
已知,如图,在△ABC中,AB=BC,D是AC的中点,BE平分∠ABD交AC于点E,点O是AB边上一点,⊙O过B、E两点,交BD于点G,交AB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com