
【题目】
已知:如图,平行四边形![]() 的对角线相交于点
的对角线相交于点![]() ,点
,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() ,联结
,联结![]() .
.
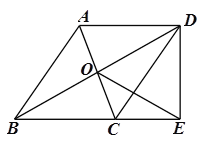
(1)求证:![]() ;
;
(2)如果![]() ,求证:
,求证:![]() .
.
【答案】(1)证明过程见解析;(2)证明过程见解析
【解析】
(1)由平行四边形的性质得到BO=![]() BD,由等量代换推出OE=
BD,由等量代换推出OE=![]() BD,根据平行四边形的判定即可得到结论;
BD,根据平行四边形的判定即可得到结论;
(2)根据等角的余角相等,得到∠CEO=∠CDE,推出△BDE∽△CDE,即可得到结论.
证明:(1)∵四边形ABCD是平行四边形,
∴BO=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠OED=∠ODE,
∵∠OBE+∠OEB+∠OED+∠ODE=180°,
∴∠BEO+∠DEO=∠BED=90°,
∴DE⊥BE;
(2)∵OE⊥CD
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵OB=OE,
∴∠DBE=∠CDE,
∵∠BED=∠BED,
∴△BDE∽△DCE,
∴![]() ,
,
∴BDCE=CDDE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
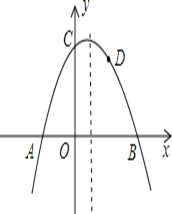
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求抛物线的解析式.
(2)若点![]() 是抛物线上一点,那么在抛物线的对称轴上,是否存在一点
是抛物线上一点,那么在抛物线的对称轴上,是否存在一点![]() ,使得
,使得![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标:若不存在,请说明理由.注:二次函数
的坐标:若不存在,请说明理由.注:二次函数![]() 的对称轴是直线
的对称轴是直线![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
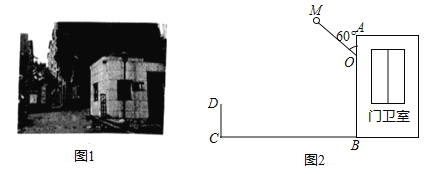
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:![]() 1.73,结果精确到0.01米)
1.73,结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.

(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛,射击队对两人的射击技能进行了测评.在相同的条件下,两人各打靶5次,成绩统计如下:

(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
(2)根据以上信息,若选派一名队员参赛,你认为应选哪名队员,并说明理由.
(3)如果标标再射击1次,命中8环,那么他射击成绩的方差会 .(填“变大”“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
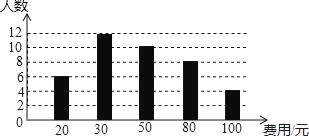
【题目】在全民读书月活动中,某校随机调查了部分同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题.
(1)这次调查获取的样本容量是 .(直接写出结果)
(2)这次调查获取的样本数据的众数是 ,中位数是 .(直接写出结果)
(3)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com