
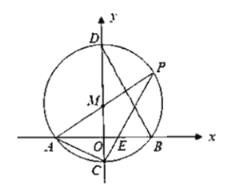
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2+8ax(a>0)гыxжсНЛгкOЃЌAСНЕуЃЌЖЅЕуЮЊMЃЌЖдГЦжсгыxжсНЛгкHЃЌгыЙ§OЃЌAЃЌMШ§ЕуЕФЁбQНЛгкЕуBЃЌЁбQЕФАыОЖЮЊ5ЃЌЕуCДгЕуBГіЗЂЃЌбизХдВжмЫГЪБеыЯђЕуMдЫЖЏЃЌЩфЯпMCгыxжсНЛгкDЃЌгыХзЮяЯпНЛгкEЃЌЙ§ЕуEзїMEЕФДЙЯпНЛХзЮяЯпЕФЖдГЦжсгкЕуF.
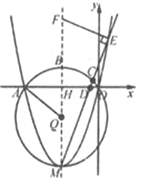
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ЕБЕуCЕФдЫЖЏТЗОЖГЄЮЊ![]() ЪБЃЌЧѓжЄЃКHD=2
ЪБЃЌЧѓжЄЃКHD=2![]() HA.
HA.
(3)дкЕуCдЫЖЏЙ§ГЬжаЃЎЪЧЗёДцдкетбљЕФЮЛжУЃЌЪЙЕУвдЕуMЃЌEЃЌFЮЊЖЅЕуЕФШ§НЧаЮгыЁїAHQЯрЫЦ?ШєДцдкЃЌЧѓГіДЫЮЛжУЪБЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁП(1)y=![]() x2+4xЃЛ(2)жЄУїМћНтЮіЃЛ(3)ДцдкЃЌE(
x2+4xЃЛ(2)жЄУїМћНтЮіЃЛ(3)ДцдкЃЌE(![]() ЃЌ
ЃЌ![]() )ЛђE(
)ЛђE(![]() ЃЌ
ЃЌ![]() )
)
ЁОНтЮіЁП
(1)РћгУКЏЪ§НтЮіЪНЃЌгЩy=0ПЩЧѓГіХзЮяЯпгыxжсЕФСННЛЕузјБъЃЌРћгУДЙОЖЖЈРэЧѓГіAHЕФГЄЃЌдйдкRtЁїAHQжаЃЌРћгУЙДЙЩЖЈРэЧѓГіHQЕФГЄЃЌгЩАыОЖЮЊ5ЃЌПЩЧѓГіЕуMЕФзјБъЃЌШЛКѓНЋЕуMЕФзјБъЕФКЏЪ§НтЮіЪНЃЌНЈСЂЙигкaЕФЗНГЬЃЌНтЗНГЬЧѓГіaЕФжЕ.
(2)РћгУЛЁГЄЙЋЪНЧѓГіnЕФжЕЃЌИљОндВжмНЧЖЈРэЧѓГіЁЯBMCЕФЖШЪ§ЃЌдкRtЁїHMDжаЃЌРћгУЙДЙЩЖЈРэЧѓГіHDЕФГЄЃЌдйИљОнMH=2AHЃЌПЩжЄЕУНсТл.
(3)ЗжЧщПіЬжТлЃКЂйЕБЁЯEMF=ЁЯHQAЪБ,ЁїMEFЁзЁїQHAЃЌРћгУЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЧѓГіHDЕФГЄЃЌПЩЕУЕНЕуDЕФзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпMDЕФКЏЪ§НтЮіЪНЃЌШЛКѓЧѓГіСНКЏЪ§ЕФНЛЕузјБъЃЛЂкЕБЁЯEMF=ЁЯQAHЪБ,ЁїMEFЁзЁїAHQЃЌРћгУЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЧѓГіHDЕФГЄЃЌПЩЕУЕНЕуDЕФзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпMDЕФКЏЪ§НтЮіЪНЃЌШЛКѓЧѓГіСНКЏЪ§ЕФНЛЕузјБъЃЌМДПЩЕУЕНЗћКЯЬтвтЕФЕуEЕФзјБъ.
НтЃК(1)Сюy=0,ЕУax2+8ax=0,НтЕУx1=-8,x2=0ЃЌ
ЁрA(-8ЃЌ0)
гЩДЙОЖЖЈРэ,ЕУAH=![]() AO=4,
AO=4,
дкRtЁїAHQжа, HQ=![]() ЃЌ
ЃЌ
ЁрHM=HQ+QM=3+5=8ЃЌ
ЁрM(-4ЃЌ-8)
АбM(-4,-8)ДњШыХзЮяЯпЕУ![]() ЃЌ
ЃЌ
НтЕУa=![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=![]() x2+4x
x2+4x
(2)ЁпЕуCЕФТЗОЖЮЊ![]() ,
,
Ёр![]() ЃЌНтЕУn=120ЁуЃЌ
ЃЌНтЕУn=120ЁуЃЌ
ЁрЁЯBMC=![]() =60Ёу,
=60Ёу,
дкRtЁїHMDжа, HD=![]() =
=![]() MH
MH
ЁпMH=8,AH=4,МДMH=2HA
ЁрHD=2![]() HA
HA
(3)ДцдкЃЌEЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() )ЃЌРэгЩШчЯТЃК
)ЃЌРэгЩШчЯТЃК
вбжЊЁЯFEM=ЁЯAHQ=90ЁуЃЌ
ЂйЕБЁЯEMF=ЁЯHQAЪБ,ЁїMEFЁзЁїQHA,
ДЫЪБЁїMHDЁзЁїQHA,
Ёр![]() ,МД
,МД![]()
НтЕУHD=![]() ЃЌ
ЃЌ
ЁрOD=![]()
ЁрD(![]() 0)ЃЌ
0)ЃЌ
ЩшжБЯпMDНтЮіЪНЮЊ![]() ЃЌНЋM(-4ЃЌ-8)ЃЌD(
ЃЌНЋM(-4ЃЌ-8)ЃЌD(![]() 0)ДњШыЕУЃЌ
0)ДњШыЕУЃЌ
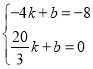 ЃЌНтЕУ
ЃЌНтЕУ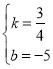 ЃЌ
ЃЌ
ЁржБЯпMDЕФНтЮіЪНЮЊy=![]() x-5,
x-5,
НЋжБЯпMDгыХзЮяЯпСЊСЂЕУЃЌ
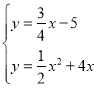 ЃЌНтЕУ
ЃЌНтЕУ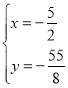 Лђ
Лђ![]()
ДЫЪБEЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
ЂкЕБЁЯEMF=ЁЯQAHЪБЃЌЁїMEFЁзЁїAHQ,
ДЫЪБЁїMHDЁзЁїAHQ,
Ёр![]() ЃЌМД
ЃЌМД![]()
НтЕУHD=6ЃЌ
ЁрOD=6-4=2
ЁрD(2,0),
ЩшжБЯпMDНтЮіЪНЮЊ![]() ЃЌНЋM(-4ЃЌ-8)ЃЌD(2ЃЌ0)ДњШыЕУЃЌ
ЃЌНЋM(-4ЃЌ-8)ЃЌD(2ЃЌ0)ДњШыЕУЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ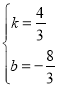 ЃЌ
ЃЌ
ЁржБЯпMDЕФНтЮіЪНЮЊ![]()
НЋжБЯпMDгыХзЮяЯпСЊСЂЕУЃЌ
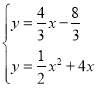 ЃЌНтЕУ
ЃЌНтЕУ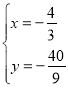 Лђ
Лђ![]()
ДЫЪБEЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
злЩЯЫљЪіЃЌEЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() ).
).


 Н№дПГзЪдОэЯЕСаД№АИ
Н№дПГзЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвдЕу![]() ЮЊдВаФЃЌзї
ЮЊдВаФЃЌзї![]() НЛ
НЛ![]() жсгк
жсгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌНЛ
СНЕуЃЌНЛ![]() жсгк
жсгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌСЌНс
СНЕуЃЌСЌНс![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЧѓЯв![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉЧѓжБЯп![]() ЕФКЏЪ§НтЮіЪНЃЛ
ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉСЌНс![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§.
ЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
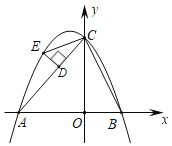
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпгызјБъжсНЛгкAЃЈЉ4ЃЌ0ЃЉЁЂBЃЈ2ЃЌ0ЃЉЁЂCЃЈ0ЃЌ4ЃЉЃЌСЌНгBCЃЌACЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуEЪЧХзЮяЯпдкЕкЖўЯѓЯоЩЯЕФвЛЕуЃЌЙ§ЕуEзїDEЁЭACгкЕуDЃЌЧѓDEЕФзюДѓжЕЃЎ
ЃЈ3ЃЉШєЕуEЪЧХзЮяЯпЩЯЕкЖўЯѓЯоЩЯЕФвЛЖЏЕуЃЌЙ§ЕуEзїDEЁЭACгкЕуDЃЌСЌНгCEЃЌШєЁїCDEгыЁїCOBЯрЫЦЃЌжБНгаДГіЕуEЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОдкМзввСНЕиЭЌЪБЯњЪлФГжжЦЗХЦЕФЦћГЕЃЌвбжЊдкМзЕиЕФзмЯњЪлРћШѓyЃЈЕЅЮЛЃКЭђдЊЃЉгыЯњЪлСПxЃЈЕЅЮЛЃКСОЃЉжЎМфТњзуyЃНЉ![]() x2+10xЃЌдкввЕиУПЯњЪлвЛСОЦћГЕПЩЛёЕУ2ЭђдЊЕФЯњЪлРћШѓЃЌШєИУЙЋЫОдкМзввСНЕиЙВЯњЪл30СОИУЦЗХЦЕФЦћГЕЃЌМзввСНЕизмЕФЯњЪлРћШѓЮЊWЭђдЊЃЌЦфжадкМзЕиЯњЪлxСОЃЎ
x2+10xЃЌдкввЕиУПЯњЪлвЛСОЦћГЕПЩЛёЕУ2ЭђдЊЕФЯњЪлРћШѓЃЌШєИУЙЋЫОдкМзввСНЕиЙВЯњЪл30СОИУЦЗХЦЕФЦћГЕЃЌМзввСНЕизмЕФЯњЪлРћШѓЮЊWЭђдЊЃЌЦфжадкМзЕиЯњЪлxСОЃЎ
ЃЈ1ЃЉЧѓWгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉМзввСНЕиИїЯњЪлЖрЩйСОГЕЪБWзюДѓЃПWЕФзюДѓжЕЪЧЖрЩйЃП
ЃЈ3ЃЉЮЊСЫПЊЭиМзЕиЪаГЁЃЌЙЋЫОЙцЖЈМзЕиЦНОљУПСОЦћГЕЕФЯњЪлРћШѓВЛИпгк2ЭђдЊЃЌФЧУДЙЋЫОЯњЪлет30СОЦћГЕПЩЛёЕУЕФзюДѓЯњЪлРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=x2-(m+1)x+mгыyжсНЛгк(0ЃЌ-3)Еу.
(1)ЧѓГіmЕФжЕКЭХзЮяЯпгыxжсЕФНЛЕуЃЛ
(2)xШЁЪВУДжЕЪБЃЌy>0.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌPAЁЂPBЮЊдВOЕФЧаЯпЃЌЧаЕуЗжБ№ЮЊAЁЂBЃЌPOНЛABгкЕуCЃЌPOЕФбгГЄЯпНЛдВOгкЕуDЃЌЯТСаНсТлВЛвЛЖЈГЩСЂЕФЪЧ( )
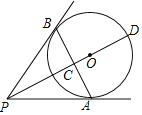
A. PAЃНPBB. ЁЯBPDЃНЁЯAPDC. ABЁЭPDD. ABЦНЗжPD
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэЯдЪОЕФЪЧФГжжДѓЖЙдкЯрЭЌЬѕМўЯТЕФЗЂбПЪдбщНсЙћЃК
УПХњСЃЪ§n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
ЗЂбПЕФСЃЪ§m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
ЗЂбПЕФЦЕТЪ | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
ЯТУцгаШ§ИіЭЦЖЯЃК
ЂйЕБnЮЊ400ЪБЃЌЗЂбПЕФДѓЖЙСЃЪ§ЮЊ382ЃЌЗЂбПЕФЦЕТЪЮЊ0.955ЃЌЫљвдДѓЖЙЗЂбПЕФИХТЪЪЧ0.955ЃЛ
ЂкЫцзХЪдбщЪБДѓЖЙЕФСЃЪ§ЕФдіМгЃЌДѓЖЙЗЂбПЕФЦЕТЪзмдк0.95ИННќАкЖЏЃЌЯдЪОГівЛЖЈЕФЮШЖЈадЃЌПЩвдЙРМЦДѓЖЙЗЂбПЕФИХТЪЪЧ0.95ЃЛ
ЂлШєДѓЖЙСЃЪ§nЮЊ4000ЃЌЙРМЦДѓЖЙЗЂбПЕФСЃЪ§ДѓдМЮЊ3800СЃЃЎ
ЦфжаЭЦЖЯКЯРэЕФЪЧЃЈЁЁЁЁЃЉ
A. ЂйЂкЂл B. ЂйЂк C. ЂйЂл D. ЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
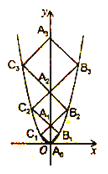
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЃЌЕу
ЕФЭМЯѓШчЭМЃЌЕу![]() ЮЛгкзјБъдЕуЃЌЕу
ЮЛгкзјБъдЕуЃЌЕу![]() дк
дк![]() жсЕФе§АыжсЩЯЃЌЕу
жсЕФе§АыжсЩЯЃЌЕу![]() дкЖўДЮКЏЪ§ЮЛгкЕквЛЯѓЯоЕФЭМЯѓЩЯЃЌЕу
дкЖўДЮКЏЪ§ЮЛгкЕквЛЯѓЯоЕФЭМЯѓЩЯЃЌЕу![]() дкЖўДЮКЏЪ§ЮЛгкЕкЖўЯѓЯоЕФЭМЯѓЩЯЃЌЫФБпаЮ
дкЖўДЮКЏЪ§ЮЛгкЕкЖўЯѓЯоЕФЭМЯѓЩЯЃЌЫФБпаЮ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЁЫФБпаЮ
ЁЫФБпаЮ![]() ЖМЪЧе§ЗНаЮЃЌдђе§ЗНаЮ
ЖМЪЧе§ЗНаЮЃЌдђе§ЗНаЮ![]() ЕФжмГЄЮЊ__________.
ЕФжмГЄЮЊ__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧ![]() ЕФжБОЖЃЌCЪЧАыдВABЩЯвЛЕуЃЌСЌACЁЂOCЃЌADЦНЗж
ЕФжБОЖЃЌCЪЧАыдВABЩЯвЛЕуЃЌСЌACЁЂOCЃЌADЦНЗж![]() ЃЌНЛЛЁBCгкDЃЌНЛOCгкEЃЌСЌODЃЌCDЃЌЯТСаНсТлЃК
ЃЌНЛЛЁBCгкDЃЌНЛOCгкEЃЌСЌODЃЌCDЃЌЯТСаНсТлЃК
ЂйЛЁ![]() ЛЁCDЃЛЂк
ЛЁCDЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂмЕБCЪЧАыдВ
ЃЛЂмЕБCЪЧАыдВ![]() ЕФжаЕуЪБЃЌдђ
ЕФжаЕуЪБЃЌдђ![]() ЃЎЦфжае§ШЗЕФНсТлЪЧЃЈ ЃЉ
ЃЎЦфжае§ШЗЕФНсТлЪЧЃЈ ЃЉ
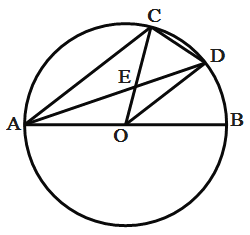
A.ЂйЂкЂлB.ЂйЂкЂмC.ЂйЂлЂмD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com