
【题目】如图所示,施工队要修建一个横断面为抛物线的公路隧道, OM宽度为16米,其顶点P到OM的距离为8米 ![]()
![]() 请建立适当的平面直角坐标系,并求出这条抛物线的函数解析式;
请建立适当的平面直角坐标系,并求出这条抛物线的函数解析式;
![]() 隧道下的公路是双向行车道
隧道下的公路是双向行车道![]() 正中间是一条宽1米的隔离带
正中间是一条宽1米的隔离带![]() ,其中的一条行车道能否行驶宽
,其中的一条行车道能否行驶宽![]() 米、高
米、高![]() 米的特种车辆?请通过计算说明.
米的特种车辆?请通过计算说明.

【答案】(1)![]() ,
,![]() ;(2)该车辆能通行;
;(2)该车辆能通行;
【解析】
(1)以O点为原点,建立直角坐标系,确定O,P,M的坐标,然后设出顶点式即可求解;
(2)由于正中有一条宽1m的隔离带,则每个车道宽7.5m,3.5m宽的车沿着隔离带边沿行驶时,车最左侧边沿的![]() ,然后将x=4代入解析式,如果函数值大于5.8,则能顺利通过.
,然后将x=4代入解析式,如果函数值大于5.8,则能顺利通过.
解: ![]() 以O点为原点,建立直角坐标系则O(0,0),P
以O点为原点,建立直角坐标系则O(0,0),P![]() ,M(0.16),且抛物线的顶点坐标为
,M(0.16),且抛物线的顶点坐标为![]() ,设函数的解析式为
,设函数的解析式为![]() ,
,
将点![]() 代入上式得:
代入上式得:![]() ,解得:
,解得:![]() ,
,
故函数的表达式为:![]() ,
,![]() ;
;
![]() 双向行车道,正中间是一条宽1米的隔离带,则每个车道宽为
双向行车道,正中间是一条宽1米的隔离带,则每个车道宽为![]() 米,
米,
车沿着隔离带边沿行驶时,车最左侧边沿的![]() ,
,
当![]() 时,
时,![]() ,即允许的最大高度为6米,
,即允许的最大高度为6米,
![]() ,故该车辆能通行;
,故该车辆能通行;


科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用,为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对八年级甲,乙两班各60名学生进行了垃极分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.
(收集数据)
甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
乙班15名学生测试成绩统计如下:《满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
(1)按如下分数段整理、描述这两组样本数据
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
甲 | 2 | 2 | 4 | 5 | 1 | 1 |
乙 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(2)补全甲班15名学生测试成绩频数分布直方图:
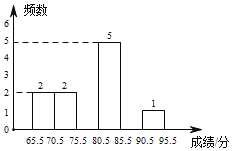
(分析数据)
(3)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 80 | x | 80 | 47.6 |
乙 | 80 | 80 | y | 26.2 |
在表中:x= ,y= .
(4)若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃极分类及投放相关知识合格的学生有 人.
(5)你认为哪个班的学生掌握垃圾分类相关知识的整体水平较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 绕某点按一定方向旋转一定角度后得到
绕某点按一定方向旋转一定角度后得到![]() ,点A,B,C分别对应点A1,B1,C1 .
,点A,B,C分别对应点A1,B1,C1 .
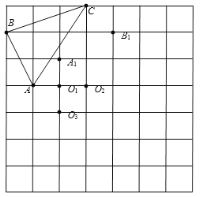
(1)根据点![]() 和
和![]() 的位置确定旋转中心是点______________.
的位置确定旋转中心是点______________.
(2)请在图中画出![]() ;
;
(3)请具体描述一下这个旋转:________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
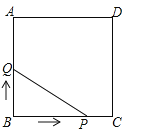
A.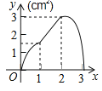 B.
B.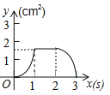 C.
C.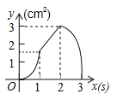 D.
D.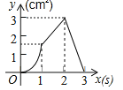
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为![]() ,连接CF,则CF= .
,连接CF,则CF= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABM=90°,⊙O分别切AB、BM于点D、E.AC切⊙O于点F,交BM于点C(C与B不重合).
(1)用直尺和圆规作出AC(保留作图痕迹,不写作法);
(2)若⊙O半径为1,AD=4,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由;
(2)如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度;
(3)若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com