
【题目】如图,∠ABM=90°,⊙O分别切AB、BM于点D、E.AC切⊙O于点F,交BM于点C(C与B不重合).
(1)用直尺和圆规作出AC(保留作图痕迹,不写作法);
(2)若⊙O半径为1,AD=4,求AC的长.

【答案】(1)见解析 (2)![]()
【解析】
(1)根据题意利用尺规作图作出AC即可;
(2)先证明矩形ODBE是正方形,再利用正方形的性质和勾股定理即可解答.
(1)如图,AC即为所求;
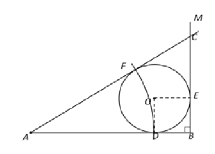
(2)解:连OD、OE.
∵ ⊙O分别切AB、BM于点D、E,
∴ OD⊥AB,OE⊥BC.
∴ ∠ODB=90°,∠OEB=90°.
又 ∠ABM=90°,
∴ 四边形ODBE是矩形.
∵ OD=OE,
∴ 矩形ODBE是正方形.
∴ BD=BE=OD=1
∵ ⊙O分别切AB、AC于点D、F,
∴ AF=AD=4.
同理 CF=CE
∵ Rt△ABC中,∠B=90°,
∴ AC2=AB2+BC2.
即 (CE+4)2=(CE+1)2+52.
解得 CE=![]() .
.
∴ AC=AF+CF=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,施工队要修建一个横断面为抛物线的公路隧道, OM宽度为16米,其顶点P到OM的距离为8米 ![]()
![]() 请建立适当的平面直角坐标系,并求出这条抛物线的函数解析式;
请建立适当的平面直角坐标系,并求出这条抛物线的函数解析式;
![]() 隧道下的公路是双向行车道
隧道下的公路是双向行车道![]() 正中间是一条宽1米的隔离带
正中间是一条宽1米的隔离带![]() ,其中的一条行车道能否行驶宽
,其中的一条行车道能否行驶宽![]() 米、高
米、高![]() 米的特种车辆?请通过计算说明.
米的特种车辆?请通过计算说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
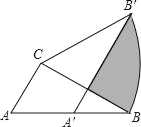
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转α角后得到△A′B′C,当点A的对应点A'落在AB边上时,旋转角α的度数是_____度,阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数![]() 的图象为C1.二次函数
的图象为C1.二次函数![]() 的图象与C1关于y轴对称.
的图象与C1关于y轴对称.

(1)求二次函数![]() 的解析式;
的解析式;
(2)当![]() ≤0时,直接写出
≤0时,直接写出![]() 的取值范围;
的取值范围;
(3)设二次函数![]() 图象的顶点为点A,与y轴的交点为点B,一次函数
图象的顶点为点A,与y轴的交点为点B,一次函数![]() ( k,m为常数,k≠0)的图象经过A,B两点,当
( k,m为常数,k≠0)的图象经过A,B两点,当![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
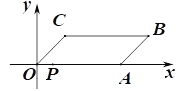
【题目】如图,平面直角坐标系中,□OABC的顶点A坐标为(6,0),C点坐标为(2,2),若经过点P(1,0)的直线平分□OABC的周长,则该直线的解析式为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到下面一个问题:
如图1所示,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求
,求![]() 的值.
的值.
小明发现,分别过![]() ,
,![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() .通过推理计算,可以解决问题(如图2).请回答,
.通过推理计算,可以解决问题(如图2).请回答,![]() ________.
________.

参考小明思考问题的方法,解决问题:
如图3,四边形![]() 中,
中,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)![]() =______.
=______.
(2)![]() =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
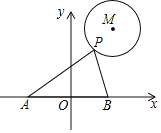
【题目】 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A. 3B. 4C. 6D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
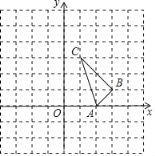
【题目】在平面直角坐标系中,已知A(2,0)、B(3,1)、C(1,3).
(1)画出△ABC沿x轴负方向平移2个单位后得到的△A1B1C1,并写出B1的坐标 ;
(2)以A1点为旋转中心,将△A1B1C1逆时针方向旋转90°得△A1B2C2,画出△A1B2C2,并写出C2的坐标 ;
(3)直接写出过B、B1、C2三点的圆的圆心坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com