
【题目】阅读下面材料:
小明遇到下面一个问题:
如图1所示,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求
,求![]() 的值.
的值.
小明发现,分别过![]() ,
,![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() .通过推理计算,可以解决问题(如图2).请回答,
.通过推理计算,可以解决问题(如图2).请回答,![]() ________.
________.

参考小明思考问题的方法,解决问题:
如图3,四边形![]() 中,
中,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)![]() =______.
=______.
(2)![]() =__________.
=__________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用,为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对八年级甲,乙两班各60名学生进行了垃极分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.
(收集数据)
甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
乙班15名学生测试成绩统计如下:《满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
(1)按如下分数段整理、描述这两组样本数据
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
甲 | 2 | 2 | 4 | 5 | 1 | 1 |
乙 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(2)补全甲班15名学生测试成绩频数分布直方图:
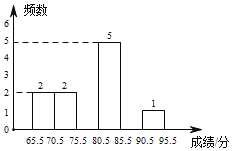
(分析数据)
(3)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 80 | x | 80 | 47.6 |
乙 | 80 | 80 | y | 26.2 |
在表中:x= ,y= .
(4)若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃极分类及投放相关知识合格的学生有 人.
(5)你认为哪个班的学生掌握垃圾分类相关知识的整体水平较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为![]() ,连接CF,则CF= .
,连接CF,则CF= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABM=90°,⊙O分别切AB、BM于点D、E.AC切⊙O于点F,交BM于点C(C与B不重合).
(1)用直尺和圆规作出AC(保留作图痕迹,不写作法);
(2)若⊙O半径为1,AD=4,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300m2的长方形围栏,围栏总长50m,一边靠墙(墙长25m).
(1)求围栏的长和宽;
(2)能否围成面积为400m2的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在边AB上,点F、E在边AC上,且DF∥BE,![]() .
.

(1)求证:DE∥BC;
(2)如果![]() ,S△ADF=2,求S△ABC的值.
,S△ADF=2,求S△ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)该抛物线的对称轴是![]() ________.
________.
(2)该抛物线与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,若此抛物线的对称轴上的点
,若此抛物线的对称轴上的点![]() 满足
满足![]() ,则点
,则点![]() 的纵坐标
的纵坐标![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由;
(2)如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度;
(3)若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.
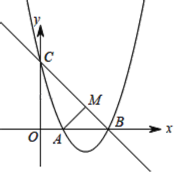

(1)求抛物线的解析式及顶点D的坐标;
(2)点P为抛物线在直线BC下方图形上的一动点,当△PBC面积最大时,求点P的坐标;
(3)若点Q为线段OC上的一动点,问:AQ+![]() QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com