
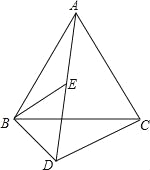
【题目】如图,已知△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明DA﹣DB=DC.
【答案】证明见解析.
【解析】试题分析:根据等边三角形的性质,可得AB与BC的关系,BD、BE、DE的关系,根据三角形全等的判定,可得△ABE与△CBD的关系,根据全等三角形的性质,可得对应边相等,根据线段的和差,等量代换,可得证明结果.
试题解析:
△ABC和△BDE都是等边三角形
∴AB=BC,BE=BD=DE(等边三角形的边相等),
∠ABC=∠EBD=60°(等边三角形的角是60°).
∴∠ABC﹣∠EBC=∠EBD﹣∠EBC
∠ABE=CBD (等式的性质),
在△ABE和△CBD中,
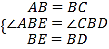 ,
,
∴△ABE≌△CBD(SAS)
∴AE=DC(全等三角形的对应边相等).
∵AD﹣DE=AE(线段的和差)
∴AD﹣BD=DC(等量代换).


科目:初中数学 来源: 题型:
【题目】如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
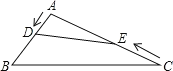
A. 4或4.8 B. 3或4.8 C. 2或4 D. 1或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班决定购买一些笔记本和文具盒做奖品.已知需要的笔记本数量是文具盒数量的3倍,购买的总费用不低于220元,但不高于250元.
(1)商店内笔记本的售价4元/本,文具盒的售价为10元/个,设购买笔记本的数量为x,按照班级所定的费用,有几种购买方案?每种方案中笔记本和文具盒数量各为多少?
(2)在(1)的方案中,哪一种方案的总费用最少?最少费用是多少元?
(3)经过还价,老板同意4元/本的笔记本可打八折,10元/个的文具盒可打七折,用(2)中的最少费用最多还可以多买多少笔记本和文具盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小云的作法如下:
(1)在直线l上任取一点B;
(2)以B为圆心,BA长为半径作弧,交直线l于点C;
(3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D;
(4)作直线AD.直线AD即为所求.

小云作图的依据是_______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
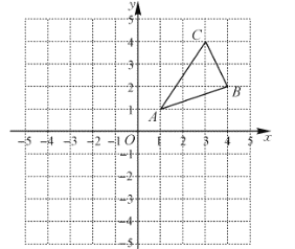
【题目】如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
A、B、C向左平移5个单位后的坐标分别为(-4,1),(-1,2),(-2,4),连接这三个点,得△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB周长最小,请画出△PAB,并直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱![]() 台,这100台家电的销售总利润为
台,这100台家电的销售总利润为![]() 元,要求购进空调数量不超过电冰箱数量的2倍,试确定获利最大的方案以及最大利润.
元,要求购进空调数量不超过电冰箱数量的2倍,试确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,∠C+∠D=210°,E、F 分别是 AD,BC 上的点,将四边形 CDEF 沿直线 EF 翻折,得到四边形 C′D′EF, C′F 交 AD 于点 G,若△EFG 有两个角相等,则∠EFG=______ °.
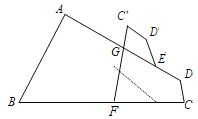
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同,正常水位时,大孔水面宽度AB=20m,顶点M距水面6m(即MO=6m),小孔顶点N距水面4.5m(即NC=4.5m),当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com