
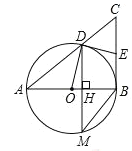
【题目】如图,在Rt△ABC中,M是斜边AB的中点,以CM为直径作圆O交AC于点N,延长MN至D,使ND=MN,连接AD、CD,CD交圆O于点E.
(1)判断四边形AMCD的形状,并说明理由;
(2)求证:ND=NE;
(3)若DE=2,EC=3,求BC的长.

【答案】(1)四边形AMCD是菱形,理由见解析;(2)证明见解析;(3)BC=2![]() .
.
【解析】
(1)证明四边形AMCD的对角线互相平分,且∠CNM=90°,可得四边形AMCD为菱形;
(2)可证得∠CMN=∠DEN,由CD=CM可证出∠CDM=∠CMN,则∠DEN=∠CDM,结论得证;
(3)证出△MDC∽△EDN,由比例线段可求出ND长,再求MN的长,则BC可求出.
(1)四边形AMCD是菱形,理由如下:
∵M是Rt△ABC中AB的中点,
∴CM=AM,
∵CM为⊙O的直径,
∴∠CNM=90°,
∴MD⊥AC,
∴AN=CN,
∵ND=MN,
∴四边形AMCD是菱形;
(2)∵四边形CENM为⊙O的内接四边形,
∴∠CEN+∠CMN=180°,
∵∠CEN+∠DEN=180°,
∴∠CMN=∠DEN,
∵四边形AMCD是菱形,
∴CD=CM,
∴∠CDM=∠CMN,
∴∠DEN=∠CDM,
∴ND=NE;
(3)∵∠CMN=∠DEN,∠MDC=∠EDN,
∴△MDC∽△EDN,
∴![]() ,
,
设DN=x,则MD=2x,由此得![]() ,
,
解得:x=![]() 或x=﹣
或x=﹣![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() ,
,
∵MN为△ABC的中位线,
∴BC=2MN,
∴BC=2![]() .
.


科目:初中数学 来源: 题型:
【题目】若一个两位数十位、个位上的数字分别为![]() ,我们可将这个两位数记为
,我们可将这个两位数记为![]() ,易知
,易知![]() ;同理,一个三位数、四位数等均可以用此记法,如
;同理,一个三位数、四位数等均可以用此记法,如![]() .
.
(基础训练)
(1)解方程填空:
①若![]() ,则
,则![]() ______;
______;
②若![]() ,则
,则![]() ______;
______;
③若![]() ,则
,则![]() ______;
______;
(能力提升)
(2)交换任意一个两位数![]() 的个位数字与十位数字,可得到一个新数
的个位数字与十位数字,可得到一个新数![]() ,则
,则![]() 一定能被______整除,
一定能被______整除,![]() 一定能被______整除,
一定能被______整除,![]() +++6一定能被______整除;(请从大于5的整数中选择合适的数填空)
+++6一定能被______整除;(请从大于5的整数中选择合适的数填空)
(探索发现)
(3)北京时间2019年4月10日21时,人类拍摄的首张黑洞照片问世,黑洞是一种引力极大的天体,连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象:任选一个三位数,要求个、十、百位的数字各不相同,把这个三位数的三个数字按大小重新排列,得出一个最大的数和一个最小的数,用得出的最大的数减去最小的数得到一个新数(例如若选的数为325,则用532-235=297),再将这个新数按上述方式重新排列,再相减,像这样运算若干次后一定会得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.
①该“卡普雷卡尔黑洞数”为______;
②设任选的三位数为![]() (不妨设
(不妨设![]() ),试说明其均可产生该黑洞数.
),试说明其均可产生该黑洞数.
查看答案和解析>>
科目:初中数学 来源: 题型:
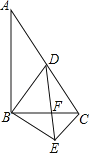
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中点,连接
的中点,连接![]() ,点
,点![]() 是
是![]() 边上的动点(不与点
边上的动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 延长线交于点
延长线交于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③![]() 和
和![]() 一定相似;
一定相似;
④若![]() ,则
,则![]() .
.
其中正确的是_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,一同学利用直尺和圆规完成如下操作:
,一同学利用直尺和圆规完成如下操作:
①以点![]() 为圆心,以
为圆心,以![]() 为半径画弧,角
为半径画弧,角![]() 于点
于点![]() ;分别以点
;分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧交点
的长为半径画弧,两弧交点![]() ,作射线
,作射线![]() ;
;
②以点![]() 为圆心,以适当的长为半径画弧,交
为圆心,以适当的长为半径画弧,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ;分别以点
;分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,作直线
,作直线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
请你观察图形,根据操作结果解答下列问题;
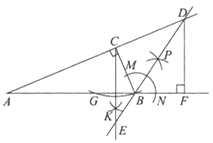
(1)线段![]() 与
与![]() 的大小关系是__________.
的大小关系是__________.
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
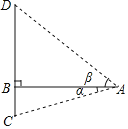
A.asinα+asinβB.acosα+acosβC.atanα+atanβD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA、CB的延长线于点E、F,连接BD.
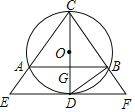
(1)求证:EF是⊙O的切线;
(2)求证:BD2=ACBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小慧家与文具店相距![]() ,小慧从家出发,沿笔直的公路匀速步行
,小慧从家出发,沿笔直的公路匀速步行![]() 来到文具店买笔记本,停留
来到文具店买笔记本,停留![]() 因家中有事,便沿着原路匀速跑步
因家中有事,便沿着原路匀速跑步![]() 返回家中.
返回家中.
![]() 小慧返回家中的速度比去文具店的速度快多少?
小慧返回家中的速度比去文具店的速度快多少?
![]() 请你画出这个过程中,小慧离家的距离
请你画出这个过程中,小慧离家的距离![]() 与时间
与时间![]() 的函数图象;
的函数图象;
![]() 根据图象回答,小慧从家出发后多少分钟离家距离为
根据图象回答,小慧从家出发后多少分钟离家距离为![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 的直角边
的直角边![]() 为直径的
为直径的![]() 交斜边
交斜边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线与
的切线与![]() 交于点
交于点![]() ,弦
,弦![]() 与
与![]() 垂直,垂足为
垂直,垂足为![]() .
.
![]() 求证:
求证:![]() 为
为![]() 的中点;
的中点;
(2)若![]() 的面积为
的面积为![]() ,两个三角形
,两个三角形![]() 和
和![]() 的外接圆面积之比为
的外接圆面积之比为![]() ,求
,求![]() 的内切圆面积
的内切圆面积![]() 和四边形
和四边形![]() 的外接圆面积
的外接圆面积![]() 的比.
的比.
查看答案和解析>>
科目:初中数学 来源: 题型:
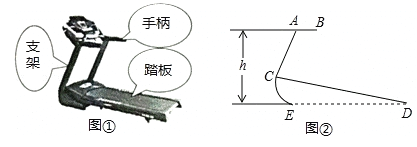
【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com