
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0.
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根;
(2)当一矩形ABCD的对角线长为AC=![]() ,且矩形两条边AB和BC恰好是这个方程的两个根时,求矩形ABCD的周长.
,且矩形两条边AB和BC恰好是这个方程的两个根时,求矩形ABCD的周长.
【答案】(1)详见解析;(2)14.
【解析】
(1)计算判别式的值得到△=(2k﹣3)2+4,利用非负数的性质得到△>0,从而根据判别式的意义得到结论;
(2)利用根与系数的关系得到AB+BC=2k+1,ABBC=4k﹣3,利用矩形的性质和勾股定理得到AB2+BC2=AC2=(![]() )2,则(2k+1)2﹣2(4k﹣3)=31,解得k1=3,k2=﹣2,利用AB、BC为正数得到k的值为3,然后计算AB+BC得到矩形ABCD的周长.
)2,则(2k+1)2﹣2(4k﹣3)=31,解得k1=3,k2=﹣2,利用AB、BC为正数得到k的值为3,然后计算AB+BC得到矩形ABCD的周长.
(1)证明:△=(2k+1)2﹣4(4k﹣3)
=4k2+4k+1﹣16k+12
=4k2﹣12k+13
=(2k﹣3)2+4,
∵(2k﹣3)2≥0,
∴△>0,
∴无论k取什么实数值,该方程总有两个不相等的实数根;
(2)根据题意得AB+BC=2k+1,ABBC=4k﹣3,
而AB2+BC2=AC2=(![]() )2,
)2,
∴(2k+1)2﹣2(4k﹣3)=31,
整理得k2﹣k﹣6=0,解得k1=3,k2=﹣2,
而AB+BC=2k+1>0,ABBC=4k﹣3>0,
∴k的值为3,
∴AB+BC=7,
∴矩形ABCD的周长为14.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
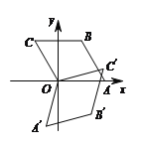
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=4,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A. (2![]() ,﹣2
,﹣2![]() )B. (
)B. (![]() ,-
,-![]() )C. (2,﹣2)D. (
)C. (2,﹣2)D. (![]() ,-
,-![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB,CD边于点E,F.
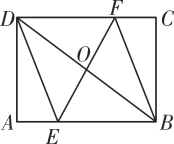
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
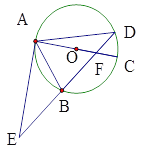
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“作已知角的角平分线”的尺规作图过程.
已知:如图,∠AOB.
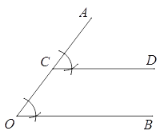
求作:∠AOB的角平分线OP.
作法:如图,
①在射线OA上任取点C;
②作∠ACD=∠AOB;
③以点C为圆心CO长为半径画圆,交射线CD于点P;
④作射线OP;
所以射线OP即为所求.
根据小元设计的尺规作图过程,完成以下任务.
(1)补全图形;
(2)完成下面的证明:
证明:∵ ∠ACD=∠AOB,
∴ CD∥OB(____________)(填推理的依据).
∴∠BOP=∠CPO.
又∵ OC=CP,
∴∠COP=∠CPO(____________)(填推理的依据).
∴∠COP=∠BOP.
∴ OP平分∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?
(3)若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com