
【题目】如图,在△ABC中,DE∥BC,EF∥AB.
(1)求证:△ADE∽△EFC;
(2)如果AB=6,AD=4,求![]() 的值.
的值.
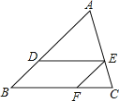
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]() :y=ax2 过点(2,2)
:y=ax2 过点(2,2)
(1)直接写出抛物线的解析式;
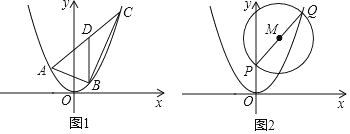
(2)如图,△ABC 的三个顶点都在抛物线![]() 上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求
上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求![]() 的值;
的值;
(3)如图,点 P 的坐标为(0,2),点 Q 为抛物线上![]() 上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况.请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,∠ABC=90°,AB=1,BC=2,将线段BC绕点C顺时旋转90°得到线段CD,连接AD.

(1)说明△ACD的形状,并求出△ACD的面积;
(2)把等腰直角三角板按如图2的方式摆放,顶点E在CB边上,顶点F在DC的延长线上,直角顶点与点C重合.从A,B两题中任选一题作答:
A .如图3,连接DE,BF,
①猜想并证明DE与BF之间的关系;②将三角板绕点C逆时针旋转α(0°<α<90°),直接写出DE与BF之间的关系.
B .将图2中的三角板绕点C逆时针旋转α(0<α<360°),如图4所示,连接BE,DF,连接点C与BE的中点M,
①猜想并证明CM与DF之间的关系;②当CE=1,CM=![]() 时,请直接写出α的值.
时,请直接写出α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(﹣1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )

A. ﹣1≤x≤9 B. ﹣1≤x<9 C. ﹣1<x≤9 D. x≤﹣1或x≥9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:
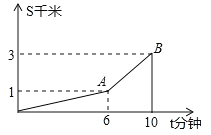
(1)小强去学校时下坡路长 千米;
(2)小强下坡的速度为 千米/分钟;
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是 分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com