
【题目】
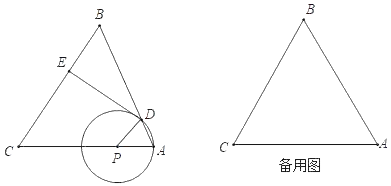
如图,△ABC中,AC=BC=10,cosC=![]() ,点P是AC边上一动点(不与点A、C重合),以PA长为半径的⊙P与边AB的另一个交点为D,过点D作DE⊥CB于点E.
,点P是AC边上一动点(不与点A、C重合),以PA长为半径的⊙P与边AB的另一个交点为D,过点D作DE⊥CB于点E.
(1)当⊙P与边BC相切时,求⊙P的半径.
(2)连接BP交DE于点F,设AP的长为x,PF的长为y,求y关于x的函数解析式,并直接写出x的取值范围.
(3)在(2)的条件下,当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时,求相交所得的公共弦的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=![]() ,则sinC=
,则sinC=![]() ,sinC=
,sinC=![]() =
=![]() =
=![]() ,即可求解;
,即可求解;
(2)首先证明PD∥BE,则![]() ,即:
,即:![]() ,即可求解;
,即可求解;
(3)证明四边形PDBE为平行四边形,则AG=EP=BD,即:AB=DB+AD=AG+AD=4![]() ,即可求解.
,即可求解.
(1)设⊙P与边BC相切的切点为H,圆的半径为R,
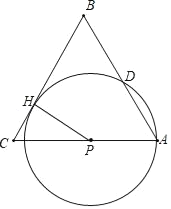
连接HP,则HP⊥BC,cosC=![]() ,则sinC=
,则sinC=![]() ,
,
sinC=![]() =
=![]() =
=![]() ,解得:R=
,解得:R=![]() ;
;
(2)在△ABC中,AC=BC=10,cosC=![]() ,
,
设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,
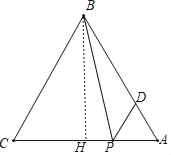
则BH=ACsinC=8,
同理可得:CH=6,HA=4,AB=4![]() ,则:tan∠CAB=2,
,则:tan∠CAB=2,
BP=![]() =
=![]() ,
,
DA=![]() x,则BD=4
x,则BD=4![]() ﹣
﹣![]() x,
x,
如下图所示,PA=PD,∴∠PAD=∠CAB=∠CBA=β,
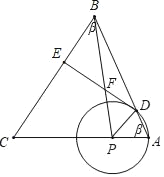
tanβ=2,则cosβ=![]() ,sinβ=
,sinβ=![]() ,
,
EB=BDcosβ=(4![]() ﹣
﹣![]() x)×
x)×![]() =4﹣
=4﹣![]() x,
x,
∴PD∥BE,
∴![]() ,即:
,即:![]() ,
,
整理得:y=![]() ;
;
(3)以EP为直径作圆Q如下图所示,
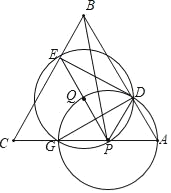
两个圆交于点G,则PG=PQ,即两个圆的半径相等,则两圆另外一个交点为D,
GD为相交所得的公共弦,
∵点Q是弧GD的中点,
∴DG⊥EP,
∵AG是圆P的直径,
∴∠GDA=90°,
∴EP∥BD,
由(2)知,PD∥BC,∴四边形PDBE为平行四边形,
∴AG=EP=BD,
∴AB=DB+AD=AG+AD=4![]() ,
,
设圆的半径为r,在△ADG中,
AD=2rcosβ=![]() ,DG=
,DG=![]() ,AG=2r,
,AG=2r,
![]() +2r=4
+2r=4![]() ,解得:2r=
,解得:2r=![]() ,
,
则:DG=![]() =50﹣10
=50﹣10![]() ,
,
相交所得的公共弦的长为50﹣10![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
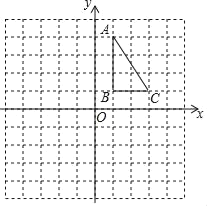
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC左平移4个单位得到的△A1B1C1,且A1的坐标为 ;
(2)画出△ABC绕点O顺时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
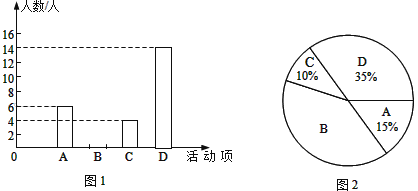
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
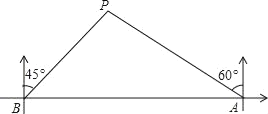
【题目】如图,在一笔直的海岸线上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿北偏西60°的方向行驶了30海里到达点P处,此时从B码头测得小船在北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生共![]() 人,为了解这个年级学生的体能,从中抽取
人,为了解这个年级学生的体能,从中抽取![]() 名学生进行
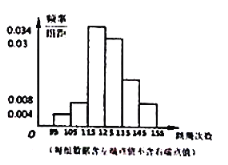
名学生进行![]() 分钟的跳绳测试,结果统计的频率分布如图所示,其中从左至右前四个小长方形的高依次为
分钟的跳绳测试,结果统计的频率分布如图所示,其中从左至右前四个小长方形的高依次为![]()
![]() ,如果跳绳次数不少于
,如果跳绳次数不少于![]() 次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为__________.
次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三点A(2,4)、B(3,5)、P(a,a),将线段AB绕点P顺时针旋转90°得到CD,其中A、B的对应点分别为C、D;
(1)当a=2时,
①在图中画出线段CD,保留作图痕迹,并直接写出C、D两点的坐标;
②将线段CD向上平移m个单位,点C、D恰好同时落在反比例函数y=![]() 的图象上,求m和k的值.
的图象上,求m和k的值.
(2)若a=4,将函数y=![]() (x>0)的图象绕点P顺时针旋转90°得到新图象,直线AB与新图象的交点为E、F,则EF的长为 .(直接写出结果)
(x>0)的图象绕点P顺时针旋转90°得到新图象,直线AB与新图象的交点为E、F,则EF的长为 .(直接写出结果)
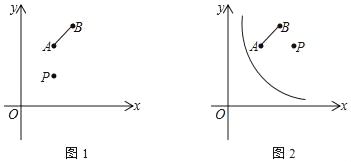
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某五金商店准备从机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用900元正好可以购进50个甲种零件和50个乙种零件.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出该五金商店本次从机械厂购进甲、乙两种零件有哪几种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com