
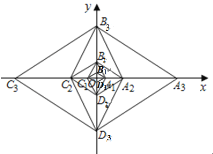
【题目】已知菱形![]() 的边长为
的边长为![]() ,
,![]() =120°,对角线
=120°,对角线![]() 相交于点
相交于点![]() ,以点
,以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴,建立如图所示的直角坐标系,以
轴,建立如图所示的直角坐标系,以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
菱形![]() ,…,按此规律继续做下去,设菱形
,…,按此规律继续做下去,设菱形![]() 的面积为
的面积为![]() ,菱形
,菱形![]() 的面积为
的面积为![]() ,…,菱形
,…,菱形![]() 的面积为
的面积为![]() ,则
,则![]() _____.
_____.
【答案】![]()
【解析】
先根据菱形的性质及锐角三角函数的定义求出OA1,OB1的长,从而可求出S1,根据相似及锐角三角函数的定义可求得OA2,OB2的长,从而可得出S2,…,找出规律即可得出结论.
解:∵菱形A1B1C1D1的边长为2,∠A1B1C1=120°,
∴∠A1B1O=60°,∠A1OC1=90°,
∴OA1=A1B1sin60°=2×![]() =
=![]() ,OB1=A1B1cos60°=2×
,OB1=A1B1cos60°=2×![]() 1,
1,
∴A1C1=2OA1=2![]() ,B1D1=2OB1=2,
,B1D1=2OB1=2,
∴S1=![]() ×A1C1×B1D1=
×A1C1×B1D1=![]() .
.
∵菱形A1B1C1D1∽菱形B2C1D2A1∽菱形![]() ,
,
∴∠A2B2C2=∠B2A1D2=∠A1B1C1=120°,
∴OB2=![]() ,
,
∴OA2=OB2×tan60°=3![]() ,B2D2=2OB2=6,
,B2D2=2OB2=6,
∴A2C2=2OA2=6![]() ,
,
∴S2=![]() ×A2C2×B2D2=
×A2C2×B2D2=![]() =2
=2![]() ×9,
×9,
同理可得,
S3=![]() ×A3C3×B3D3=
×A3C3×B3D3=![]() ,
,
S4=![]() ×A4C4×B4D4=
×A4C4×B4D4=![]() ,
,
…
∴Sn=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色相同,则甲获胜;若两次指针指到的颜色是黄绿组合则乙获胜;其余情况则视为平局.
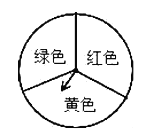
(1)请用画树状图或列表的方法,写出所有可能出现的结果;
(2)试用概率说明游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的含30°角的三角尺如图①摆放在一起,设较短的直角边长为3.
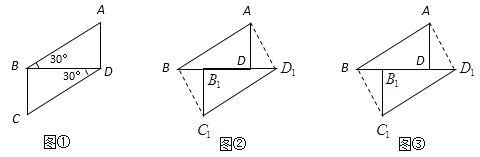
(1)四边形ABCD是平行四边形吗?说出你的结论和理由.
(2)如图②,将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置,四边形ABC1D1是平行四边形吗?说出你的结论和理由.
(3)在Rt△BCD沿射线BD方向平移的过程中,当点B的移动距离为多少时四边形ABC1D1为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
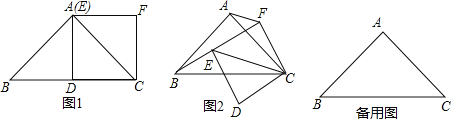
【题目】(1)如图1,在![]() 中,
中,![]() 90°,点
90°,点![]() 为
为![]() 的中点,以
的中点,以![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 恰好与点
恰好与点![]() 重合,则线段
重合,则线段![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)在(1)的条件下,如果正方形![]() 绕点
绕点![]() 旋转,连接
旋转,连接![]() ,
,
①线段![]() 与
与![]() 的数量关系有无变化?请仅就图2的情形给出证明;
的数量关系有无变化?请仅就图2的情形给出证明;
②当正方形![]() 旋转到
旋转到![]() 三点共线时,直接写出线段
三点共线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
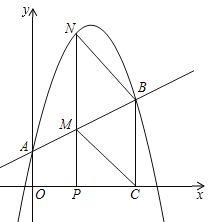
【题目】如图,抛物线![]() 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒令是中国民间风俗之一.白居易曾诗曰:“花时同醉破春愁,醉折花枝当酒筹”饮酒行令,是中国人在饮酒时助兴的一种特有方式,不仅要以酒助兴,往往还伴之以赋诗填词、猜迷形拳之举,最早诞生于西周,完备于隋唐,“虎棒鸡虫令”是其中一种:“二人相对,以筷子相声,同时或喊虎、喊棒、喊鸡、喊虫,以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负,负者饮.若棒兴鸡、或虫兴虎同时出现(解释:若棒与鸡,虎与虫同时喊出)或两人喊出同一物,则不分胜负,继续喊”.依据上述规则,张三和李四同时随机地喊出其中一物,两人只喊一次.
(1)求张三喊出“虎”取胜的概率;
(2)用列表法或画树状图法,求李四取胜的概率;
(3)直接写出两人能分出胜负的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
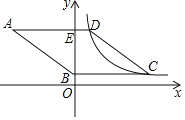
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com