
【题目】如图,将锐角为![]() 的直角三角板MPN的一个锐角顶点P与边长为4的正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,
的直角三角板MPN的一个锐角顶点P与边长为4的正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,![]() 的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.在三角板旋转过程中,当
的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.在三角板旋转过程中,当![]() 的一边恰好经过BC边的中点时,则EF的长为_____.
的一边恰好经过BC边的中点时,则EF的长为_____.

【答案】![]() 或
或![]()
【解析】
①当MA经过BC的中点E时,延长FD至G,使DG=BE,连接AG,先证△ABE≌△ADG,再证△GAF≌△EAF,利用勾股定理列出方程即可;②NA经过BC的中点H时,在CD上截取DQ=BE,连接AQ,同理证明△ABE≌△ADQ(SAS),再证明△QAF≌△EAF(SAS)和△ABH≌△FCH(ASA),根据勾股定理列出方程即可解决问题.
解:①当MA经过BC的中点E时,延长FD至G,使DG=BE,连接AG,如下图所示,
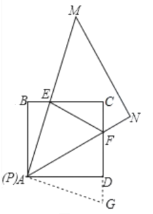
∵ABCD是正方形,
∴AB=AD,∠ABE=∠ADG=∠DAB=90°,
又∵BE=DG,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠DAG=∠EAB,
∵∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠DAF+∠DAG=45°,
∴∠GAF=∠EAF=45°,
∵AF=AF,
∴△GAF≌△EAF,
∴EF=GF,
∴GF=DF+DG=DF+BE,
∴EF=DF+BE.
∵点E是BC的中点,
∴BE=CE=2,
设FD=x,则FG=EF=2+x,FC=4x.
在Rt△EFC中,(x+2)2=(4x)2+22,
∴x=![]() ,
,
∴EF=x+2=![]() .
.
②当NA经过BC的中点H时,在CD上截取DQ=BE,连接AQ,如下图所示,
由情况①可知,△ABE≌△ADQ(SAS),
∴AE=AQ,∠DAQ=∠EAB,
∴∠DAQ+∠BAQ=∠EAB+∠BAQ=90°,
∵∠EAF=45°,
∴∠QAF=∠EAF=45°,
∵AF=AF,
∴△QAF≌△EAF(SAS),
∴EF=QF,
又∵点H是BC的中点,
∴BH=CH,
∵∠ABH=∠FCH,∠BHA=∠CHF,
∴△ABH≌△FCH(ASA),
∴CF=AB=4,
设BE=DQ=x,则EC=4+x,EF=QF=8x,
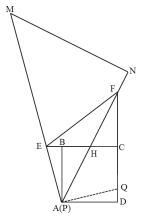
∵CH=BH=2,CF=AB=4,
由勾股定理得到:(4+x)2+42=(8x)2,
∴x=![]() ,
,
∴EF=8![]() =
=![]()
综上所述,EF的长为![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】把下面的推理过程补充完整,并在括号内注明理由.
如图,已知∠B+∠BCD=180°,∠B=∠D.
试说明:∠E=∠DFE
解:∠B+∠BCD=180°(已知)
∴AB∥CD( )
∴∠B=∠DCE( )
又∵∠B=∠D(已知)
∴∠DCE= ( )
∴AD∥BE( )
∴∠E=∠DFE( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解一元二次方程时,发现有这样一种解法:
如:解方程![]() .
.
解:原方程可变形,得: ![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
直接开平方并整理,得. ![]() ,
, ![]() .
.
我们称小明这种解法为“平均数法”.
(1)下面是小明用“平均数法”解方程![]() 时写的解题过程.
时写的解题过程.
解:原方程可变形,得: ![]() .
.
![]() ,
,
![]() .
.
直接开平方并整理,得. ![]() ,
, ![]() .
.
上述过程中的a、b、c、d表示的数分别为 , , , .
(2)请用“平均数法”解方程: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程,解应用题
甲乙两人相约周末到影院看电影,他们的家分别距离影院1200米和2000米,两人分别从家中同时出发,已知甲和乙的速度比是![]() ,结果甲比乙提前4分钟到达影院.
,结果甲比乙提前4分钟到达影院.
(1)求甲、乙两人的速度?
(2)在看电影时,甲突然接到家长电话让其15分钟内赶回家,时间紧迫改变速度,比来时每分钟多走25米,甲是否能按要求时间到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A,B两种产品共50件,生产A,B两种产品与所需原料情况如下表所示:
原料 型号 | 甲种原料(千克) | 乙种原料(千克) |
A产品(每件) | 9 | 3 |
B产品(每件) | 4 | 10 |
(1)该工厂生产A,B两种产品有哪几种方案?
(2)如果该工厂生产一件A产品可获利80元,生产一件B产品可获利120元,那么该工厂应该怎样安排生产可获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题
(1)抽取了______名学生成绩;(2)请把条形统计图补充完整;
(3)扇形统计图中等级D所在的扇形的圆心角度数是______;
(4)若A,B,C代表合格,该校初二年级有300名学生,求全年级生物合格的学生共约多少人

查看答案和解析>>
科目:初中数学 来源: 题型:
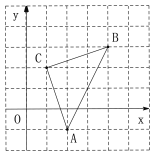
【题目】如图,直角坐标系中,三角形ABC的顶点都在网格点上,其中A(2,![]() ), B(4,3), C(1,2).
), B(4,3), C(1,2).
(1)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形![]() ,则三角形
,则三角形![]() 的三个顶点坐标。
的三个顶点坐标。![]() ( ),
( ),![]() ( ),
( ),![]() ( ).
( ).
(2)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=2cm,AE=1cm,求⊙O的半径.
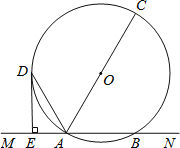
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com