
【题目】如图,直线y=2x﹣8分别交x轴、y轴于点A、点B,抛物线y=ax2+bx(a≠0)经过点A,且顶点Q在直线AB上.

(1)求a,b的值.
(2)点P是第四象限内抛物线上的点,连结OP、AP、BP,设点P的横坐标为t,△OAP的面积为s1,△OBP的面积为s2,记s=s1+s2,试求s的最值.
【答案】(1)![]() ;(2)当t=3时,s取得最大值,最大值为18.
;(2)当t=3时,s取得最大值,最大值为18.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标,由二次函数的对称性可得出抛物线的对称轴为直线x=2,利于一次函数图象上点的坐标特征可求出抛物线的顶点Q的坐标,由点A,P的坐标,利用待定系数法即可求出a,b的值;
(2)利用二次函数图象上点的坐标特征可得出点P的坐标,利用三角形的面积公式可找出s1,s2,进而可得出s关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
解:(1)∵直线y=2x﹣8分别交x轴、y轴于点A、点B,
∴点A的坐标为(4,0),点B的坐标为(0,﹣8).
∵抛物线y=ax2+bx(a≠0)经过点A,点O,
∴抛物线的对称轴为直线x=2.
当x=2时,y=2x﹣8=﹣4,
∴抛物线顶点Q的坐标为(2,﹣4).
将A(4,0),Q(2,﹣4)代入y=ax2+bx,得:
![]() ,解得:
,解得:![]() .
.
(2)由(1)得:抛物线解析式为y=x2﹣4x,
∵点P的横坐标为t,
∴点P的坐标为(t,t2﹣4t),
∴s1=![]() ×4×(4t﹣t2)=8t﹣2t2,s2=
×4×(4t﹣t2)=8t﹣2t2,s2=![]() ×8×t=4t,
×8×t=4t,
∴s=s1+s2=﹣2t2+12t=﹣2(t﹣3)2+18.
∵﹣2<0,且0<t<4,
∴当t=3时,s取得最大值,最大值为18.



科目:初中数学 来源: 题型:
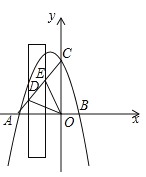
【题目】如图,抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为半圆的直径,点
为半圆的直径,点![]() 为圆心,
为圆心,![]() 为半圆的切线,过半圆上的点
为半圆的切线,过半圆上的点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)连接![]() ,若
,若![]() ,求证:
,求证:![]() 是半圆的切线;
是半圆的切线;
(2)如图2,当线段![]() 与半圆交于点
与半圆交于点![]() 时,连接
时,连接![]() ,
,![]() ,判断
,判断![]() 和
和![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月12日是我国义务植树节。某校组织学生开展义务植树活动,在活动结束后随机调查了40名学生每人植树的棵数,根据调查获取的样本数据,制作了不完整的扇形统计图和条形统计图.请根据相关信息,解答下列问题:

(Ⅰ)扇形统计图中m的值是_____________,补全条形统计图
(Ⅱ)求抽取的这部分学生植树棵数的平均数;
(Ⅲ)若本次活动共有320名学生参加,估计植树棵数超过8棵的约有多少人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春暖花开,树木萌芽,某种时令蔬菜的价格呈上升趋势,若这种蔬菜开始时的售价为每斤20元,并且每天涨价2元,从第六天开始,保持每斤30元的稳定价格销售,直到11天结束,该蔬菜退市.
(1)请写出该种蔬菜销售价格y与天数x之间的函数关系式;
(2)若该种蔬菜于进货当天售完,且这种蔬菜每斤进价z与天数x的关系为z=﹣![]() +12(1≤x≤11),且x为整数,那么该种蔬菜在第几天售出后,每斤获得利润最大?最大利润为多少?
+12(1≤x≤11),且x为整数,那么该种蔬菜在第几天售出后,每斤获得利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() .有下列结论:①
.有下列结论:①![]() ; ②当
; ②当![]() 时,随x的增大而增大;③当
时,随x的增大而增大;③当![]() 时,
时,![]() ;④当
;④当![]() 时,若二次函数的最小值为
时,若二次函数的最小值为![]() ,则m的取值范围是
,则m的取值范围是![]() 。其中正确结论的个数是( )
。其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y ax2 bx c a 0经过点 A2, 0、 B 5, 0.
(1)用含 a 的代数式表示b 、c ;
(2)若点C 6, 4在抛物线上,在抛物线上找一点 P ,使 x 轴恰好平分CAP ,若存在求出点 P ,并求出此时ACP 的面积;
(3)在(2)的条件下,在抛物线的对称轴上是否存在一点Q,使tan AQC 2 ,若存在求出点Q 的坐标,若不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com