
【题目】已知抛物线 y ax2 bx c a 0经过点 A2, 0、 B 5, 0.
(1)用含 a 的代数式表示b 、c ;
(2)若点C 6, 4在抛物线上,在抛物线上找一点 P ,使 x 轴恰好平分CAP ,若存在求出点 P ,并求出此时ACP 的面积;
(3)在(2)的条件下,在抛物线的对称轴上是否存在一点Q,使tan AQC 2 ,若存在求出点Q 的坐标,若不存在请说明理由.

【答案】(1)b=-3a, c=-10a (2) P(4,3);![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)把A2, 0、 B 5, 0代入解析式可得方程组,求解可得答案;
(2)将C 6, 4代入,求得函数解析式,设存在点![]() ,使x 轴恰好平分CAP,则点P关于X轴的对称点Q在AC上,,且
,使x 轴恰好平分CAP,则点P关于X轴的对称点Q在AC上,,且![]() ,求出直线AC解析式,再将点Q坐标代入,可得m的值,则得到P(4,3),进而得到三解形ACP的面积;
,求出直线AC解析式,再将点Q坐标代入,可得m的值,则得到P(4,3),进而得到三解形ACP的面积;
(3)由 tan AQC 2 得 ![]() ,在Rt△ACE中,
,在Rt△ACE中, ![]() ,设△ACQ的外接圆圆心为D(m,n),连接AD交圆D于P,则APC=AQC,∠ACP=90° ,
,设△ACQ的外接圆圆心为D(m,n),连接AD交圆D于P,则APC=AQC,∠ACP=90° ,![]() ,在Rt△ACP中,
,在Rt△ACP中,![]() ,得△ACQ的外接圆直径
,得△ACQ的外接圆直径![]() ,半径为5.设△ACQ的外接圆圆心为D(m,n),可得到方程组
,半径为5.设△ACQ的外接圆圆心为D(m,n),可得到方程组![]() ,解方程组得到D的坐标为D(1,-4)或(3,0),再利用勾股定理解Rt△DHQ,得到QH的长,进而得到点Q的坐标.
,解方程组得到D的坐标为D(1,-4)或(3,0),再利用勾股定理解Rt△DHQ,得到QH的长,进而得到点Q的坐标.
(1)把A2, 0、 B 5, 0代入解析式可得:
![]()
解得b=-3a, c=-10a
(2) 由点C 6, 4在抛物线上,得

解得![]() ,
,![]() ,
,![]()
故解析式为![]()
如图,设存在点![]() ,使x 轴恰好平分CAP,则点P关于X轴的对称点Q在AC上,,且
,使x 轴恰好平分CAP,则点P关于X轴的对称点Q在AC上,,且![]() ,
,
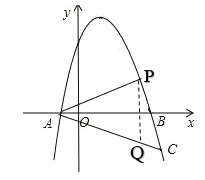
∵A(-2,0),C(6,-4),
∴可得直线AC的解析式为:![]()
∴![]()
解得![]()
∴P(4,3)
∴![]()
(3)如图,过点C作CE⊥x轴于点E,
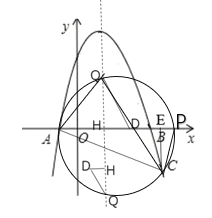
∵ tan AQC 2
∴ ![]()
∵A(-2,0),C(6,-4),
∴AE=8,CE=4
在Rt△ACE中, ![]()
设△ACQ的外接圆圆心为D(m,n),连接AD交圆D于P,则
APC=AQC,∠ACP=90°,
∴![]()
在Rt△ACP中![]()
∴AP![]()
∴圆D的半径为5
∴AD=DC=5,
∴![]()
解得![]()
当D(1,-4)时,
在Rt△DHQ中,DH=![]() ,DQ=5,
,DQ=5,
∴![]()
∴![]()
当D(3,0)时,
在Rt△DHQ中,DH=![]() ,DQ=5,
,DQ=5,
∴![]()
∴![]()
综上所述,点![]() 或
或![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
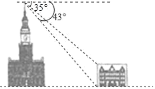
【题目】如图,甲、乙两座建筑物的水平距离BC为30m,从甲的顶部A处测得乙的顶部D处的俯角为35°测得底部C处的俯角为43°,求甲、乙两建筑物的高度AB和DC(结果取整数).
(参考数据:tan35°≈0.70,tan43°≈0.93)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x﹣8分别交x轴、y轴于点A、点B,抛物线y=ax2+bx(a≠0)经过点A,且顶点Q在直线AB上.

(1)求a,b的值.
(2)点P是第四象限内抛物线上的点,连结OP、AP、BP,设点P的横坐标为t,△OAP的面积为s1,△OBP的面积为s2,记s=s1+s2,试求s的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
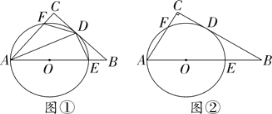
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接市教育局开展的“创先争优”主题演讲活动,某校组织党员教师进行演讲预赛.学校将所有参赛教师的成绩(得分为整数,满分为100分)分成四组,绘制了不完整的统计图表如下:
组别 | 成绩x | 组中值 | 频数 |
第一组 | 90≤x≤100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | |
第三组 | 70≤x<80 | 75 | 8 |
第四组 | 60≤x<70 | 65 |
观察图表信息,回答下列问题:
(1)参赛教师共有 人;
(2)如果将各组的组中值视为该组的平均成绩,请你估算所有参赛教师的平均成绩;
(3)成绩落在第一组的恰好是两男两女四位教师,学校从中随机挑选两位教师参加市教育局组织的决赛.通过列表或画树状图求出挑选的两位教师是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组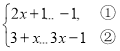
请结合题意填空,完成本题的解答。
(I)解不等式①,得________________
(Ⅱ)解不等式②,得:_____________________
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
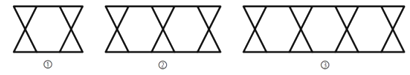
A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
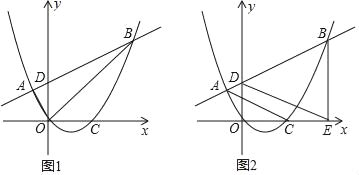
【题目】如图,抛物线y=ax2+bx经过点A(﹣1,![]() )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)识图理解:
请认真观察如图给出的未来一周某市的每天的最高气温和最低气温,直接回答后面提出的问题:
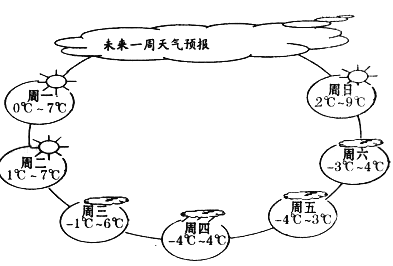
(1)这一周该市的最高气温和最低气温分别是多少?
(2)这一周中,星期几的温差最大?是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com