
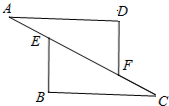
 如图,在△ADF与△CBE中,点A、E、F、C在同一直线上,已知AD∥BC,AD=CB,AE=CF.求证:DF=BE.
如图,在△ADF与△CBE中,点A、E、F、C在同一直线上,已知AD∥BC,AD=CB,AE=CF.求证:DF=BE. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
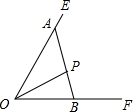 如图,∠EOF内有一定点P,过点P的一条直线分别交射线OE于A,射线OF于B.当满足下列哪个条件时,△AOB的面积一定最小( )
如图,∠EOF内有一定点P,过点P的一条直线分别交射线OE于A,射线OF于B.当满足下列哪个条件时,△AOB的面积一定最小( )| A、OA=OB |
| B、OP为△AOB的角平分线 |
| C、OP为△AOB的高 |
| D、OP为△AOB的中线 |
查看答案和解析>>
科目:初中数学 来源: 题型:
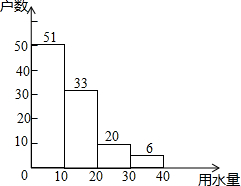 某小区300户家庭,从中随机抽取了100户,调查了他们5月份的用水量情况,结果如图所示.
某小区300户家庭,从中随机抽取了100户,调查了他们5月份的用水量情况,结果如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com