
 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���ͼ����x�ᣬy��ֱ��ڵ�A��8��0����B��0��4������C������Ϊ��3��0��������D������BO��һ�����㣬����CD������C��CD��FC����һ�κ���ͼ���ڵ�F��
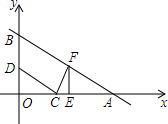
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���ͼ����x�ᣬy��ֱ��ڵ�A��8��0����B��0��4������C������Ϊ��3��0��������D������BO��һ�����㣬����CD������C��CD��FC����һ�κ���ͼ���ڵ�F������ ��1�����ô���ϵ�������ɵ�A��8��0����B��0��4���������ֱ�߽���ʽ��
��2����OCD���EFCȫ�ȷ�Ϊ�����������ȫ�ȵó��߶�EF��CE���ȣ����������F�ĺ�����������꣬����ֱ�߽���ʽ�Ϳ��������F�����꣮
��3����ACF�ǵ��������Σ����Է�����������ۣ����ݵ����������������F������꣮
��� �⣺��1����һ�κ�������ʽΪy=kx+b��k��0��k��bΪ��������
����A��8��0����B��0��4������ã�
$\left\{\begin{array}{l}{0=8k+b}\\{b=4}\end{array}\right.$��
��ã�k=-$\frac{1}{2}$��b=4��
��һ�κ�������ʽΪ��y=-$\frac{1}{2}$x+4��
��2���ߡ�OCD���EFCȫ�ȣ�
����Է������������OCD�ա�EFC���OCD�ա�ECF��
�ٵ���OCD�ա�EFCʱ��
OC=EF=3��
���F������Ϊ3��
��y=3����ֱ�߽���ʽ�ã�x=2��
��F��2��3����
�ڵ���OCD�ա�ECF��
OC=EC=3��
���F������Ϊ6��
��x=6����ֱ�߽���ʽ�ã�y=1��
��F��6��1����
��F����������2��3����6��1����
��3�����ڣ�
��ACF�ǵ��������Σ�
�ٵ�CF=AFʱ��
���ݵ������������ߺ�һ���ʣ��õ�EΪAC�е㣬
AC=5��CE=$\frac{5}{2}$��
��OE=$\frac{11}{5}$����F�������Ϊ$\frac{11}{5}$��
��x=$\frac{11}{5}$����һ�κ�����y=$\frac{29}{10}$
��F��$\frac{11}{5}$��$\frac{29}{10}$����
�ڵ�AF=ACʱ��OB=4��OA=8��
AB=4$\sqrt{5}$��
��EF��OB��
���AEF�ס�AOB��
��$\frac{AF}{AB}$=$\frac{EF}{OB}$��
��ã�EF=$\sqrt{5}$��
��y=$\sqrt{5}$����ֱ�߽���ʽ���ã�x=8-2$\sqrt{5}$��
��F��8-2$\sqrt{5}$��$\sqrt{5}$����
�۵�CF=AC=5ʱ��
��OC=3��OB=4��
��BC=5��
��ʱ��CB=CF����F���B�غϣ�
���P��������y�Ḻ���ᣬ�����ⲻ������ȥ��
���F��������$\frac{11}{5}$��$\frac{29}{10}$������8-2$\sqrt{5}$��$\sqrt{5}$����
���� ���⿼����һ�κ������ۺ�Ӧ�á�ȫ�������С����������ε�֪ʶ��֪ʶ���漰�϶࣬��Ŀ������ѣ��ر�����Ŀ���ڶ���������ڽ����������ʱ��ע�ⲻҪ����©��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �·� | 1 | 2 | 3 | 4 |
| ��ˮ�����֣� | 6 | 8 | 12 | 15 |
| ���ã�Ԫ�� | 12 | 16 | 28 | 37 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
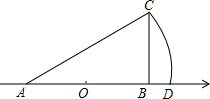 ��ͼ�������ϵ�A��ʾ������-1��ԭ��O���߶�AB���е㣬��BAC=30�㣬��ABC=90�㣬�Ե�AΪԲ�ģ�ACΪ�뾶�������������ڵ�D�����D��ʾ�����ǣ�������
��ͼ�������ϵ�A��ʾ������-1��ԭ��O���߶�AB���е㣬��BAC=30�㣬��ABC=90�㣬�Ե�AΪԲ�ģ�ACΪ�뾶�������������ڵ�D�����D��ʾ�����ǣ�������| A�� | $\frac{2\sqrt{3}}{3}-1$ | B�� | $\frac{2\sqrt{3}}{3}$ | C�� | $\frac{4\sqrt{3}}{3}$ | D�� | $\frac{4\sqrt{3}}{3}-1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
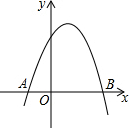 ������y=ax2+bx+c��a��0����x�����������ֱ�ΪA��-1��0����B��2��0������һԪ���η���ax2+bx+c=0�Ľ�Ϊx1=-1��x2=2��
������y=ax2+bx+c��a��0����x�����������ֱ�ΪA��-1��0����B��2��0������һԪ���η���ax2+bx+c=0�Ľ�Ϊx1=-1��x2=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���е������������������ϵĵ��ʾ | |
| B�� | ���Ų�ͬ����������Ϊ�෴�� | |
| C�� | ���������������� | |
| D�� | ������ӣ���һ�������κ�һ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9.6��10 | B�� | 96��104 | C�� | 9.6��105 | D�� | 9.6��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCDEF�У���A=��D����B=��E����C=��F����֤��AF��CD��AB��DE��BC��EF��
��ͼ��������ABCDEF�У���A=��D����B=��E����C=��F����֤��AF��CD��AB��DE��BC��EF���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com