
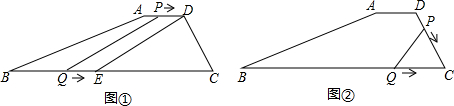
分析 (1)求出CE长度,根据平行四边形对边平行且相等,建立等量关系:PD=QE,根据题意建立方程求解即可;
(2)过点P作PM⊥BC,用t表示出CP,CQ,PM,进一步表示三角形面积即可;
(3)分情况表示出三角形PQC的面积,求出梯形面积,根据题意建立方程即可求解;
(4)求出x与t的关系,代入(2)中关系式即可求解.
解答 解:(1)不存在,理由如下:
∵DE⊥CD,∠C=60°,DC=6cm,
∴∠CED=30°,
∴CE=2CD=12,
设点P、Q运动的时间是t(s),PD=4-t,QE=BC-CE-BQ=20-12-2t=8-2t,
使四边形PQED是平行四边形,
有PD=QE,
∴4-t=8-2t,
解得:t=4,此时点P与点D重合,不能构成平行四边形;
(2)如图②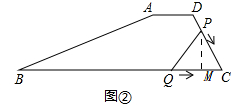
由题意可求:PC=10-t,QC=20-2t,
过点P作PM⊥BC,
∵∠C=60°,
∴$\frac{PM}{PC}$=sin60°=$\frac{\sqrt{3}}{2}$,
可求PM=$\frac{\sqrt{3}}{2}$(10-t),
∴S=$\frac{1}{2}$×(20-2t)×$\frac{\sqrt{3}}{2}$(10-t)=$\frac{\sqrt{3}}{2}$t2-$10\sqrt{3}t$+$50\sqrt{3}$;
(3)如图3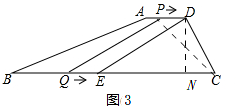
过点D作DN⊥BC,
由DC=6,∠DCB=60°,可求:DN=$3\sqrt{3}$,
∴梯形ABCD的面积为:(4+20)×$3\sqrt{3}$÷2=$36\sqrt{3}$,
当t≤4时,QC=20-2t,
此时,△PQC的面积为:(20-2t)×$3\sqrt{3}$÷2,
由题意得:(20-2t)×$3\sqrt{3}$÷2=$36\sqrt{3}$×$\frac{2}{9}$,
解得:t=$\frac{22}{3}$(舍去);
当4<t≤10时,
由(2)知,△PQC的面积为:$\frac{\sqrt{3}}{2}$t2-$10\sqrt{3}t$+$50\sqrt{3}$,
由题意:$\frac{\sqrt{3}}{2}$t2-$10\sqrt{3}t$+$50\sqrt{3}$=$36\sqrt{3}$×$\frac{2}{9}$,
解得:t=6,或t=14(舍去),
所以当t=6时,△PQC的面积是梯形ABCD的面积的$\frac{2}{9}$;
(4)如图②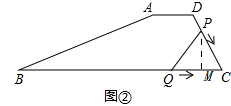
由(2)知:PC=10-t,QC=20-2t,
过点P作PM⊥BC,
∵∠C=60°,
∴$\frac{PM}{PC}$=sin60°=$\frac{\sqrt{3}}{2}$,
PM=$\frac{\sqrt{3}}{2}$(10-t),
可求:CM=$\frac{1}{2}$(10-t),QM=QC-CM=$\frac{3}{2}$(10-t),
由勾股定理可求:PQ=$\sqrt{3}$(10-t),
当PQ=x时,$\sqrt{3}$(10-t)=x,解得:t=10-$\frac{\sqrt{3}}{3}x$,
∴S=$\frac{1}{2}$×(20-2t)×$\frac{\sqrt{3}}{2}$(10-t)=$\frac{\sqrt{3}}{6}{x}^{2}$,
点评 此题主要考察四边形的综合问题,会根据平行四边形的性质研究点的存在问题,会用变量表示三角形面积,会运用方程解决相关问题是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,在梯形ABCD中AB∥CD,对角线AC、BD交于点O,△ABC为边长为6的等边三角形,DC=2.
已知如图,在梯形ABCD中AB∥CD,对角线AC、BD交于点O,△ABC为边长为6的等边三角形,DC=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.767×105 | B. | 6.676×1012 | C. | 6.676×1013 | D. | 6.676×1014 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+m | B. | $\frac{ma}{m+n}$ | C. | $\frac{a}{m+n}$ | D. | $\frac{m+n}{am}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两枚骰子的点数的和可能为11 | B. | 两枚骰子的点数不可能相同 | ||
| C. | 两枚骰子的点数一定相同 | D. | 两枚骰子的点数的差可能为6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com