

分析 (1)解两函数解析式组成的方程组即可;
(2)求出Q的坐标,设出解析式,把Q、C的坐标代入求出即可;
(3)过C作CM⊥OA于M,根据三角形的面积公式解答即可;
(4)分为两种情况,画出图形,根据等腰三角形的性质求出即可
解答 解:(1)∵由$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
∴C(2,2);
(2)如图1: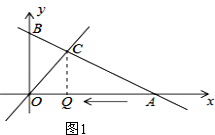
令$-\frac{1}{2}x+3=0$,得x=6,A(6,0)
由题意:Q(3,0),
设直线CQ的解析式是y=kx+b,
把C(2,2),Q(3,0)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{2k+b=2}\end{array}\right.$,
解得:k=-2,b=6,y=-2x+6;
(3)如图2: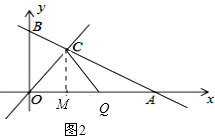
∵C(2,2),过C作CM⊥OA于M,
∵C(2,2),
∴CM=2,
∴S△PAC=$\frac{1}{2}$CMⅹPA=$\frac{1}{2}$ⅹ2ⅹPA=8,
∴PA=8,
∴P的坐标为(-2,0)或(14,0).
(4)①、CO为底时,Q为顶点时,如图3,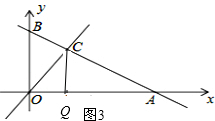
当∠COQ=45°,CQ=OQ,
∵C(2,2),
∴OQ=CQ=2,
∴AQ=OA-OQ=6-2=4,
②CO为腰时,C为顶点时,如图4,过C作CM⊥OA于M,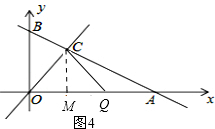
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴AQ=OA-OQ=2,即t的值为2
③CO为底时,O为顶点时,如图5: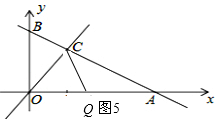
OQ=OC=$2\sqrt{2}$,
AQ=AO-OQ=6-$2\sqrt{2}$或AQ=AO+OQ=6+$2\sqrt{2}$.
故答案为:t的值为2或4或6-$2\sqrt{2}$或6+$2\sqrt{2}$.
点评 本题考查了用待定系数法求出一次函数解析式,三角形的面积,等腰直角三角形等知识点的应用,题目是一道比较典型的题目,综合性比较强.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形OABC放置在平面直角坐标系中,OA所在直线为x轴,OC所在直线为y轴,且OA=4,OC=2.当直线y=-x+b(0≤b≤6)中的b从0开始逐渐变大时,在矩形上扫过的面积记为S,则S关于b的函数图象是( )
如图,矩形OABC放置在平面直角坐标系中,OA所在直线为x轴,OC所在直线为y轴,且OA=4,OC=2.当直线y=-x+b(0≤b≤6)中的b从0开始逐渐变大时,在矩形上扫过的面积记为S,则S关于b的函数图象是( )| A. | 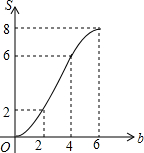 | B. |  | C. | 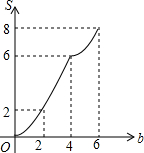 | D. | 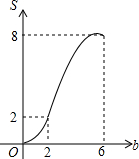 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com