
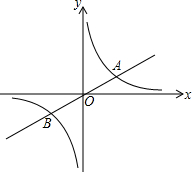
 反比例函数y=
反比例函数y=| k |
| x |
| ||
| 3 |
| 6 |
| ||
| 3 |
| ||
| 3 |
| 6 |
| k |
| x |
| ||
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 6 |
(x+x)2+(
|
| 6 |
3
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
| k |
| x |
3
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2x |
3
| ||
| 2x |
3
| ||
| 2 |
| ||
| 2 |
(
|
| 6 |
| 6 |
| x2+y2 |
| 6 |
| y+y2 |
| 6 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
|
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、随意掷一枚均匀的硬币两次,至少有一次反面朝上 |
| B、今年冬天黑龙江会下雪 |
| C、随意掷两个均匀的骰子,朝上面的点数之和为1 |
| D、一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域 |
查看答案和解析>>
科目:初中数学 来源: 题型:
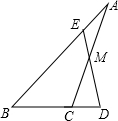 如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=
如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=| 1 |
| 4 |
| A、2:1 | B、3:2 |
| C、3:1 | D、5:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com