
【题目】问题探究:小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请你解决相关问题:
![]() 在函数
在函数![]() 中,自变量x可以是任意实数;
中,自变量x可以是任意实数;
![]() 如表y与x的几组对应值:
如表y与x的几组对应值:
X |
|
|
|
|
| 0 | 1 | 2 | 3 | 4 |
|
Y |
|
| 0 | 1 | 2 | 3 | 2 | 1 | a |
|
|
![]() ______;
______;
![]() 若
若![]() ,
,![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ______;
______;
![]() 如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
![]() 该函数有______
该函数有______![]() 填“最大值”或“最小值”
填“最大值”或“最小值”![]() ;并写出这个值为______;
;并写出这个值为______;
![]() 求出函数图象与坐标轴在第二象限内所围成的图形的面积;
求出函数图象与坐标轴在第二象限内所围成的图形的面积;
![]() 观察函数
观察函数![]() 的图象,写出该图象的两条性质.
的图象,写出该图象的两条性质.
【答案】(2)![]() 0;
0;![]() ;(3)①最大值,3;②
;(3)①最大值,3;②![]() ;③函数图象为轴对称图形,对称轴为y轴;当
;③函数图象为轴对称图形,对称轴为y轴;当![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() 时,y随x增大而减小.
时,y随x增大而减小.
【解析】
![]() 将
将![]() 代入函数解析式即可求得a;
代入函数解析式即可求得a;
![]() 当
当![]() 时,根据函数解析式可求得b;
时,根据函数解析式可求得b;
![]() 根据题意画出函数图象,根据图象特征即可求得题目所求.
根据题意画出函数图象,根据图象特征即可求得题目所求.
解:![]() 当
当![]() 时,求得
时,求得![]() ;
;
![]() 由题意,当
由题意,当![]() 时,得
时,得![]() ,解得:
,解得:![]() 或
或![]() ,所以
,所以![]() .
.
![]() 函数图象如下图所示:
函数图象如下图所示:
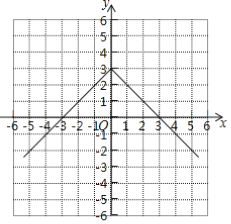
![]() 由图知,该函数有最大值3;
由图知,该函数有最大值3;
![]() 由图知,函数图象与x轴负半轴的交点为
由图知,函数图象与x轴负半轴的交点为![]() ,与y轴正半轴的交点为
,与y轴正半轴的交点为![]() ,
,
因此函数图象在第二象限内所围成的图形的面积为:![]() ,
,
![]() 由图象知可知函数
由图象知可知函数![]() 有如下性质:
有如下性质:
函数图象为轴对称图形,对称轴为y轴;当![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() 时,y随x增大而减小.
时,y随x增大而减小.
故答案为:(2)![]() 0;
0;![]() ;(3)①最大值,3;②
;(3)①最大值,3;②![]() ;③函数图象为轴对称图形,对称轴为y轴;当
;③函数图象为轴对称图形,对称轴为y轴;当![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() 时,y随x增大而减小.
时,y随x增大而减小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
①试说明BE·AD=CD·AE;
②根据图形特点,猜想![]() 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.
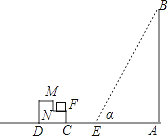
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
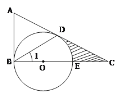
【题目】如图,在△ABC中,∠ABC= 90°,D是边AC上的一点,AB= AD,连接BD, E是BC上的一点,以BE为直径的⊙0经过点D.
(1)求证: AC是⊙O的切线:
(2)若∠A=60°,⊙O的半径为2,求CE长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)点![]() ,
,![]() 在该函数的图象上,比较
在该函数的图象上,比较![]() 与
与![]() 的大小;
的大小;
(3)将直线![]() 向下平移3个单位,与直线
向下平移3个单位,与直线![]() 交于
交于![]() 点,求点
点,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第![]() 档次的产品一天的总利润为
档次的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且1≤
为正整数,且1≤![]() ≤10),求出
≤10),求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() (x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
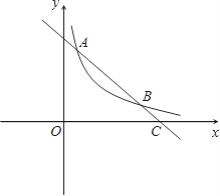
(1)求反比例函数和一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)根据图象直接写出在第一象限内反比例函数值大于一次函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经营甲、乙两种商品,两种商品的进价和售价情况如下表:
进价(万元/件) | 售价(万元/件) | |
甲 | 12 | 14.5 |
乙 | 8 | 10 |
两种商品的进价和售价始终保持不变.现准备购进甲、乙两种商品共20件.设购进甲种商品![]() 件,两种商品全部售出可获得利润为
件,两种商品全部售出可获得利润为![]() 万元.
万元.
(1)![]() 与
与![]() 的函数关系式为__________________;
的函数关系式为__________________;
(2)若购进两种商品所用的资金不多于200万元,则该公司最多购进多少合甲种商品?
(3)在(2)的条件下,请你帮该公司设计一种进货方案,使得该公司获得最大利润,并求出最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com