
【题目】设双曲线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第三象限),将双曲线在第一象限的一支沿射线
在第三象限),将双曲线在第一象限的一支沿射线![]() 的方向平移,使其经过点
的方向平移,使其经过点![]() ,将双曲线在第三象限的一支沿射线
,将双曲线在第三象限的一支沿射线![]() 的方向平移,使其经过点
的方向平移,使其经过点![]() ,平移后的两条曲线相交于点
,平移后的两条曲线相交于点![]() ,
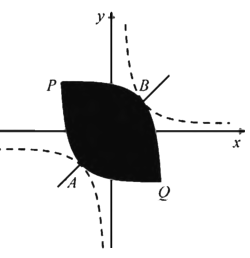
,![]() 两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,
两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,![]() 为双曲线的“眸径”.当双曲线
为双曲线的“眸径”.当双曲线![]() 的眸径为6时,
的眸径为6时,![]() 的值为__________.
的值为__________.
【答案】![]()
【解析】以PQ为边,作矩形PQQ′P′交双曲线于点P′、Q′,联立直线AB及双曲线解析式成方程组,通过解方程组可求出点A、B的坐标,由PQ的长度可得出点P的坐标(点P在直线y=-x上找出点P的坐标),由图形的对称性结合点A、B和P的坐标可得出点P′的坐标,再利用反比例函数图象上点的坐标特征即可得出关于k的一元一次方程,解之即可得出结论.
以PQ为边,作矩形PQQ′P′交双曲线于点P′、Q′,如图所示.
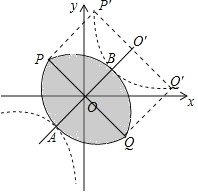
联立直线AB及双曲线解析式成方程组,![]() ,
,
解得: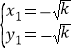 ,
,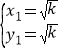 ,
,
∴点A的坐标为(-![]() ,-
,-![]() ),点B的坐标为(
),点B的坐标为(![]() ,
,![]() ).
).
∵PQ=6,
∴OP=3,点P的坐标为(-![]() ,
,![]() ).
).
根据图形的对称性可知:AB=OO′=PP′,
∴点P′的坐标为(-![]() +2
+2![]() ,
,![]() +2
+2![]() ).
).
又∵点P′在双曲线y=![]() 上,
上,
∴(-![]() +2
+2![]() )(
)(![]() +2
+2![]() )=k,
)=k,
解得:k=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】新定义:[a,b,c]为二次函数y=ax2+bx+e(a≠0,a,b,c为实数)的“图象数”,如:y=-x2+2x+3的“图象数”为[-1,2,3]
(1)二次函数y=![]() x2-x-1的“图象数”为 .
x2-x-1的“图象数”为 .
(2)若图象数”是[m,m+1,m+1]的二次函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )

A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
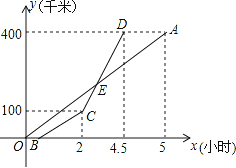
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 是定长线段
是定长线段![]() 上一定点.点
上一定点.点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发,分别以
出发,分别以![]() /
/![]() 、
、![]() /
/![]() 的速度沿直线
的速度沿直线![]() 同时向左运动.
同时向左运动.
(1)若![]() ,当点
,当点![]() 、
、![]() 运动了
运动了![]() ,求
,求![]() 的值;
的值;
(2)若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,则
,则![]() _____
_____![]() ;
;
(3)在(2)的条件下,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
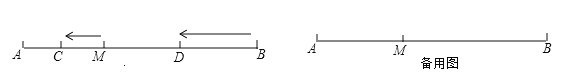
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条24cm的细绳围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
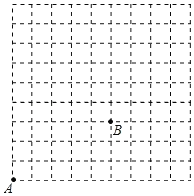
【题目】如图,在9×9的方格(每小格边长为1个单位)中,有格点A,B现点A沿网格线跳动规定:向右跳动一格需要m秒,向上跳动一格需要n秒,且每次跳动后均落在格点上.
(1)点A跳到点B,需要 秒(用含m,n的代数式表示).
(2)已知m=1,n=2.
①若点A向右跳动3秒,向上跳动10秒到达点C,请在图中标出点C的位置,并求出以BC为边的正方形的面积.
②若点A跳动5秒到达点D,请直接写出点D与点B之间距离的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )
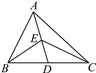
A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
已知:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
试说明:∠EGF=90°.
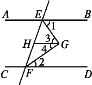
解:因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+ =180°( ).
又因为EG平分∠BEF(已知),
所以∠1=![]() ∠ ( ).
∠ ( ).
又因为FG平分∠EFD(已知),
所以∠2=![]() ∠ ( ),
∠ ( ),
所以∠1+∠2=![]() ( + ).
( + ).
所以∠1+∠2=90°.
所以∠3+∠4=90°( ),即∠EGF=90°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com