
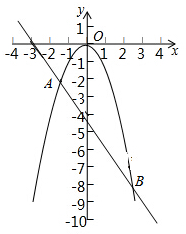 如图所示,抛物线y1=-x2与直线y2=-$\frac{3}{2}x-\frac{9}{2}$交于A,B两点.
如图所示,抛物线y1=-x2与直线y2=-$\frac{3}{2}x-\frac{9}{2}$交于A,B两点.分析 (1)利用抛物线方程和直线方程列出方程-$\frac{3}{2}x-\frac{9}{2}$=-x2,通过解方程求得点A、B的横坐标,然后根据函数图象上点的坐标特征求得相应的纵坐标;
(2)(3)结合图象可以直接得到答案;
(4)运用割补法将三角形补成一个直角梯形,进行解答即可.
解答 解:(1)由题意得,-$\frac{3}{2}x-\frac{9}{2}$=-x2,
解得x1=3,x2=-$\frac{3}{2}$.
将其分别代入y1=-x2得到:y1=-9或y1=-$\frac{9}{4}$.
故A(-$\frac{3}{2}$,-$\frac{9}{4}$),B(3,-9);
(2)结合图象知,当自变量x的取值范围为x<0时,y1的值随x的增大而增大;
(3)结合图象知,当自变量x的取值范围为-$\frac{3}{2}$<x<3时,y1<y2;
(4)由A(-$\frac{3}{2}$,-$\frac{9}{4}$),B(3,-9)知,
S△ABO=$\frac{1}{2}$×($\frac{9}{4}$+9)×(3+$\frac{3}{2}$)-$\frac{1}{2}$×$\frac{9}{4}$×$\frac{3}{2}$-$\frac{1}{2}$×3×9=$\frac{81}{8}$.
故答案是:(1)x<0;(2)-$\frac{3}{2}$<x<3.
点评 此题考查二次函数的性质,一次函数与二次函数的交点问题,两个函数联立方程是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB,AP,BD,AD分别交于点M,E,F,N.
在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB,AP,BD,AD分别交于点M,E,F,N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一段圆弧过网格的格点A,B,C,若在网格中建立平面直角坐标系,使点A的坐标为(0,-3),点C的坐标为(3,0),则该圆弧所在圆的圆心坐标为( )
如图,一段圆弧过网格的格点A,B,C,若在网格中建立平面直角坐标系,使点A的坐标为(0,-3),点C的坐标为(3,0),则该圆弧所在圆的圆心坐标为( )| A. | (-1,1) | B. | (0,-1) | C. | (1,-1) | D. | (1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 缩小到原分式值的$\frac{1}{10}$ | ||
| C. | 缩小到原分式值的$\frac{1}{100}$ | D. | 缩小到原分式值的$\frac{1}{1000}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1×10-3米 | B. | 1×10-4米 | C. | 1×10-6米 | D. | 1×10-7米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com