
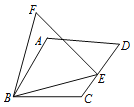
【题目】如图7,在四边形ABCD中,AB=BC,∠ABC=60°,E是CD边上一点,连接BE,以BE为一边作等边三角形BEF.请用直尺在图中连接一条线段,使图中存在经过旋转可完全重合的两个三角形,并说明这两个三角形经过什么样的旋转可重合.
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为![]() ,则a的值是( )
,则a的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+4与x轴、y轴分别交于点A、B,M是y轴上的点(不与点B重合),若将△ABM沿直线AM翻折,点B恰好落在x轴正半轴上,则点M的坐标为( )
x+4与x轴、y轴分别交于点A、B,M是y轴上的点(不与点B重合),若将△ABM沿直线AM翻折,点B恰好落在x轴正半轴上,则点M的坐标为( )
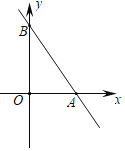
A.(0,﹣4 )B.(0,﹣5 )C.(0,﹣6 )D.(0,﹣7 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:凡购买原价超过200元的商品,超过200元的部分可以享受打折优惠若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)之间的函数关系的a图象如图所示,则图中a的值是( )

A.300B.320C.340D.360
查看答案和解析>>
科目:初中数学 来源: 题型:
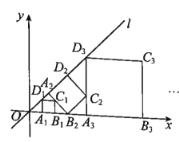
【题目】如图,在平面直角坐标系中,直线l为正比例函数![]() 的图象,点
的图象,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作x轴的垂线交直线l于点
作x轴的垂线交直线l于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作直线l的垂线,垂足为
作直线l的垂线,垂足为![]() ,交x轴于点
,交x轴于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作x轴的垂线,垂足为
作x轴的垂线,垂足为![]() ,交直线l于点
,交直线l于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;……按此规律操作下去,得到的正方形
;……按此规律操作下去,得到的正方形![]() 的面积是______________.
的面积是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
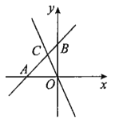
【题目】如图,在平面直角坐标系中,![]() 为坐标原点.一次函数的图象与x轴交于点
为坐标原点.一次函数的图象与x轴交于点![]() ,与y轴交于点B,与正比例函数
,与y轴交于点B,与正比例函数![]() 的图象交于点
的图象交于点![]() .
.
(1)求一次函数的解析式;
(2)在x轴上寻找点P,使得![]() 为等腰三角形,直接写出所有满足条件的点P的坐标;
为等腰三角形,直接写出所有满足条件的点P的坐标;
(3)在直线AB上寻找点Q,使得![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
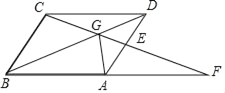
【题目】已知菱形ABCD中,AB=8,点G是对角线BD上一点,CG交BA的延长线于点F.
(1)求证:CG2=GEGF;
(2)如果DG=![]() GB,且AG⊥BF,求cos∠F.
GB,且AG⊥BF,求cos∠F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com