
ΓΨΧβΡΩΓΩΘ®1Θ©Θ®≤ΌΉςΖΔœ÷Θ©
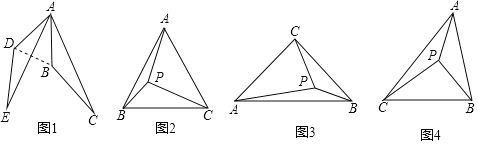
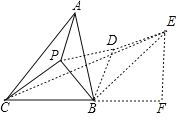
»γΆΦ1Θ§ΫΪΓςABC»ΤΒψAΥ≥ ±’κ–ΐΉΣ50ΓψΘ§ΒΟΒΫΓςADEΘ§Ν§Ϋ”BDΘ§‘ρΓœABDΘΫΓΓ ΓΓΕ»Θ°
Θ®2Θ©Θ®ΫβΨωΈ ΧβΘ©
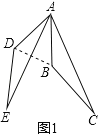
ΔΌ»γΆΦ2Θ§‘Ύ±Ώ≥ΛΈΣ![]() ΒΡΒ»±Ώ»ΐΫ«–ΈABCΡΎ”–“ΜΒψPΘ§ΓœAPCΘΫ90ΓψΘ§ΓœBPCΘΫ120ΓψΘ§«σΓςAPCΒΡΟφΜΐΘ°
ΒΡΒ»±Ώ»ΐΫ«–ΈABCΡΎ”–“ΜΒψPΘ§ΓœAPCΘΫ90ΓψΘ§ΓœBPCΘΫ120ΓψΘ§«σΓςAPCΒΡΟφΜΐΘ°
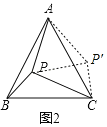
ΔΎ»γΆΦ3Θ§‘ΎΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ACΘΫBCΘ§P «ΓςABCΡΎΒΡ“ΜΒψΘ§»τPBΘΫ1Θ§PAΘΫ3Θ§ΓœBPCΘΫ135ΓψΘ§‘ρPCΘΫΓΓ ΓΓΘ°
Θ®3Θ©Θ®ΆΊ’Ι”Π”ΟΘ©
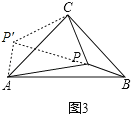
»γΆΦ4 «AΘ§BΘ§C»ΐΗω¥εΉ”ΈΜ÷ΟΒΡΤΫΟφΆΦΘ§Ψ≠≤βΝΩABΘΫ4Θ§BCΘΫ3![]() Θ§ΓœABCΘΫ75ΓψΘ§PΈΣΓςABCΡΎΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”PAΘ§PBΘ§PCΘ°«σPA+PB+PCΒΡΉν–Γ÷ΒΘ°
Θ§ΓœABCΘΫ75ΓψΘ§PΈΣΓςABCΡΎΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”PAΘ§PBΘ§PCΘ°«σPA+PB+PCΒΡΉν–Γ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©65ΘΜΘ®2Θ©ΔΌ![]() ΘΜΔΎ2ΘΜΘ®3Θ©PA+PB+PCΒΡΉν–Γ÷ΒΈΣ
ΘΜΔΎ2ΘΜΘ®3Θ©PA+PB+PCΒΡΉν–Γ÷ΒΈΣ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΓΨ≤ΌΉςΖΔœ÷ΓΩΘΚ»γΆΦ1÷–Θ§ΗυΨί–ΐΉΣΒΡ–‘÷ Ω…ΒΟADΘΫABΘ§”…Β»±ΏΕ‘Β»Ϋ«ΚΆ»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΩ…«σ≥ω¥πΑΗΘΜ
Θ®2Θ©ΓΨΫβΨωΈ ΧβΓΩ
ΔΌ»γΆΦ2÷–Θ§ΫΪΓςAPB»ΤΒψAΑ¥Ρφ ±’κΖΫœρ–ΐΉΣ60ΓψΘ§ΒΟΒΫΓςAPΓδCΓδΘ§÷Μ“Σ÷ΛΟςΓœPPΓδCΘΫ90ΓψΘ§άϊ”ΟΙ¥Ι…Ε®άμΦ¥Ω…ΫβΨωΈ ΧβΘΜ
ΔΎ»γΆΦ3÷–Θ§ΫΪΓςCBP»ΤΉ≈ΒψCΑ¥Υ≥ ±’κΖΫœρ–ΐΉΣ90ΓψΘ§ΒΟΒΫΓςCAPΓδΘ§ΗυΨί–ΐΉΣΒΡ–‘÷ Ω…“‘ΒΟΒΫΓœPΓδCPΘΫΓœACBΘΫ90ΓψΘ§ΫχΕχΒΟΒΫΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«σ≥ωPP'Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
Θ®3Θ©ΓΨΆΊ’Ι”Π”ΟΓΩ
»γΆΦ4÷–Θ§ΫΪΓςAPB»ΤBCΥ≥ ±’κ–ΐΉΣ60ΓψΘ§ΒΟΒΫΓςEDBΘ§Ν§Ϋ”PDΓΔCEΘ°ΒΟ≥ωΓœCBEΘΫ135ΓψΘ§ΙΐΒψEΉςEFΓΆCBΫΜCBΒΡ―”≥ΛœΏ”ΎΒψFΘ§«σ≥ωCFΚΆEFΒΡ≥ΛΘ§Ω…«σ≥ωCE≥ΛΘ§‘ρ¥πΑΗΩ…«σ≥ωΘ°
Θ®1Θ©ΓΨ≤ΌΉςΖΔœ÷ΓΩ
ΫβΘΚ»γΆΦ1÷–Θ§
ΓΏΓςABC»ΤΒψAΥ≥ ±’κ–ΐΉΣ50ΓψΘ§ΒΟΒΫΓςADEΘ§
ΓύADΘΫABΘ§ΓœDABΘΫ50ΓψΘ§
Γύ![]() ΘΫ65ΓψΘ§
ΘΫ65ΓψΘ§
Ι ¥πΑΗΈΣΘΚ65Θ°
Θ®2Θ©ΓΨΫβΨωΈ ΧβΓΩ
ΔΌΫβΘΚ»γΆΦ2÷–Θ§ΓΏΫΪΓςAPB»ΤΒψAΑ¥Ρφ ±’κΖΫœρ–ΐΉΣ60ΓψΘ§ΒΟΒΫΓςAPΓδCΓδΘ§
ΓύΓςAPPΓδ «Β»±Ώ»ΐΫ«–ΈΘ§ΓœAPΓδCΘΫΓœAPBΘΫ360Γψ©¹90Γψ©¹120ΓψΘΫ150ΓψΘ§
ΓύPPΓδΘΫAPΘ§ΓœAPΓδPΘΫΓœAPPΓδΘΫ60ΓψΘ§
ΓύΓœPPΓδCΘΫ90ΓψΘ§ΓœPΓδPCΘΫ30ΓψΘ§
ΓύPPΓδΘΫ![]() PCΘ§Φ¥APΘΫ
PCΘ§Φ¥APΘΫ![]() PCΘ§
PCȧ
ΓΏΓœAPCΘΫ90ΓψΘ§
ΓύAP2+PC2ΘΫAC2Θ§Φ¥Θ®![]() PCΘ©2+PC2ΘΫΘ®
PCΘ©2+PC2ΘΫΘ®![]() Θ©2Θ§
Θ©2Θ§
ΓύPCΘΫ2Θ§
ΓύAPΘΫ![]() Θ§
Θ§
ΓύSΓςAPCΘΫ![]() APPCΘΫ
APPCΘΫ![]() ΓΝ
ΓΝ![]() ΓΝ2ΘΫ
ΓΝ2ΘΫ![]() Θ°
Θ°
ΔΎ»γΆΦ3Θ§ΫΪΓςCBP»ΤΉ≈ΒψCΑ¥Υ≥ ±’κΖΫœρ–ΐΉΣ90ΓψΘ§ΒΟΒΫΓςCAPΓδΘ§
ΓΏCPΓδΘΫCPΘ§ΓœPΓδCPΘΫΓœACBΘΫ90ΓψΘ§
ΓύΓςPΓδCPΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύΓœCP'PΘΫ45ΓψΘ§
ΓΏΓœBPCΘΫ135ΓψΘΫΓœAP'CΘ§
ΓύΓœAPΓδPΘΫ90ΓψΘ§
ΓΏPAΘΫ3Θ§PBΘΫ1Θ§
ΓύAPΓδΘΫ1Θ§
ΓύPPΓδΘΫ![]() ΘΫ
ΘΫ![]() ΘΫ2
ΘΫ2![]() Θ§
Θ§
ΓύPCΘΫ![]() ΘΫ
ΘΫ![]() ΘΫ2Θ°
ΘΫ2Θ°
Ι ¥πΑΗΈΣΘΚ2Θ°
Θ®3Θ©ΓΨΆΊ’Ι”Π”ΟΓΩ
ΫβΘΚ»γΆΦ4÷–Θ§ΫΪΓςAPB»ΤBΥ≥ ±’κ–ΐΉΣ60ΓψΘ§ΒΟΒΫΓςEDBΘ§Ν§Ϋ”PDΓΔCEΘ°
ΓΏΫΪΓςAPB»ΤBΥ≥ ±’κ–ΐΉΣ60ΓψΘ§ΒΟΒΫΓςEDBΘ§
ΓύΓœABPΘΫΓœEBDΘ§ABΘΫEBΘΫ4Θ§ΓœPBDΘΫ60ΓψΘ§ΓςBPDΈΣΒ»±Ώ»ΐΫ«–ΈΘ§AP=DE
ΓύΓœABP+ΓœPBCΘΫΓœEBD+ΓœPBCΘ§PB=PD
ΓύΓœEBD+ΓœPBCΘΫΓœABCΘΫ75ΓψΘ§ΗυΨίΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΩ…ΒΟPA+PB+PC=DEΘΪPDΘΪPCΓήCEΘ§Φ¥PA+PB+PCΒΡΉν–Γ÷ΒΈΣCEΒΡ≥Λ
ΓύΓœCBEΘΫ135ΓψΘ§
ΙΐΒψEΉςEFΓΆCBΫΜCBΒΡ―”≥ΛœΏ”ΎΒψFΘ§
ΓύΓœEBFΘΫ45ΓψΘ§
Γύ![]() Θ§
Θ§
‘ΎRtΓςCFE÷–Θ§ΓΏΓœCFEΘΫ90ΓψΘ§BCΘΫ3![]() Θ§EFΘΫ2
Θ§EFΘΫ2![]() Θ§
Θ§
Γύ![]() ΘΫ
ΘΫ![]()
Φ¥PA+PB+PCΒΡΉν–Γ÷ΒΈΣ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§ΥΡ±Ώ–Έ
÷–Θ§ΥΡ±Ώ–Έ![]() ΈΣ’ΐΖΫ–ΈΘ§Βψ
ΈΣ’ΐΖΫ–ΈΘ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ―Ί±Ώ
―Ί±Ώ![]() ¥”
¥”![]() œρ
œρ![]() “‘ΟΩΟκ
“‘ΟΩΟκ![]() ΒΡΥΌΕ»‘ΥΕ·Θ§Ά§ ±Ε·Βψ
ΒΡΥΌΕ»‘ΥΕ·Θ§Ά§ ±Ε·Βψ![]() ―Ί±Ώ
―Ί±Ώ![]() ¥”
¥”![]() œρ
œρ![]() “‘Ά§―υΒΡΥΌΕ»‘ΥΕ·Θ§Ν§Ϋ”
“‘Ά§―υΒΡΥΌΕ»‘ΥΕ·Θ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() .
.
Θ®1Θ© ‘ΧΫΥςœΏΕΈ![]() ΓΔ
ΓΔ![]() ΒΡΙΊœΒΘ§–¥≥ωΡψΒΡΫα¬έ≤ΔΥΒΟςάμ”…ΘΜ
ΒΡΙΊœΒΘ§–¥≥ωΡψΒΡΫα¬έ≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§Ζ÷±π»Γ
Θ§Ζ÷±π»Γ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Θ§‘ρΥΡ±Ώ–Έ
Θ§‘ρΥΡ±Ώ–Έ![]() « ≤Ο¥ΧΊ βΤΫ––ΥΡ±Ώ–ΈΘΩ«κ‘ΎΆΦΔΌ÷–≤Ι»ΪΆΦ–ΈΘ§≤ΔΥΒΟςάμ”….
« ≤Ο¥ΧΊ βΤΫ––ΥΡ±Ώ–ΈΘΩ«κ‘ΎΆΦΔΌ÷–≤Ι»ΪΆΦ–ΈΘ§≤ΔΥΒΟςάμ”….
Θ®3Θ©»γΆΦΔΎΒ±Βψ![]() ‘ΥΕ·ΒΫ
‘ΥΕ·ΒΫ![]() ÷–Βψ ±Θ§Βψ
÷–Βψ ±Θ§Βψ![]() «÷±œΏ
«÷±œΏ![]() …œ»Έ“β“ΜΒψΘ§Βψ
…œ»Έ“β“ΜΒψΘ§Βψ![]() «ΤΫΟφΡΎ»Έ“β“ΜΒψΘ§ «Ζώ¥φ‘ΎΒψ
«ΤΫΟφΡΎ»Έ“β“ΜΒψΘ§ «Ζώ¥φ‘ΎΒψ![]() Ι“‘
Ι“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψ
ΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
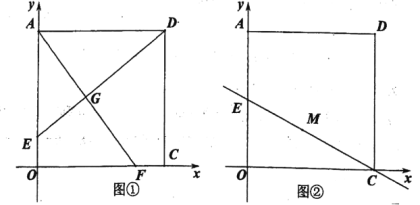
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷Σ≈ΉΈοœΏ![]() (aΘΦ0)”κx÷αΫΜ”ΎAΓΔBΝΫΒψ(ΒψA‘ΎΒψBΉσ≤ύ)Θ§”κy÷αΗΚΑκ÷αΫΜ”ΎΒψCΘ§ΕΞΒψΈΣDΘ§“―÷Σ
(aΘΦ0)”κx÷αΫΜ”ΎAΓΔBΝΫΒψ(ΒψA‘ΎΒψBΉσ≤ύ)Θ§”κy÷αΗΚΑκ÷αΫΜ”ΎΒψCΘ§ΕΞΒψΈΣDΘ§“―÷Σ![]() ΘΚSΥΡ±Ώ–ΈACBD=1ΘΚ4Θ°
ΘΚSΥΡ±Ώ–ΈACBD=1ΘΚ4Θ°
Θ®1Θ©«σΒψDΒΡΉχ±ξ(”ΟΫωΚ§cΒΡ¥ζ ΐ Ϋ±μ Ψ)ΘΜ
Θ®2Θ©»τtanΓœACB=![]() Θ§«σ≈ΉΈοœΏΒΡΫβΈω ΫΘ°
Θ§«σ≈ΉΈοœΏΒΡΫβΈω ΫΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Β»―ϋ»ΐΫ«–ΈΓςABC÷–Θ§ΓœBAC=120ΓψΘ§AB=3Θ°
Θ®1Θ©«σBCΒΡ≥ΛΘ°
Θ®2Θ©»γΆΦΘ§ΒψD‘ΎCAΒΡ―”≥ΛœΏ…œΘ§DEΓΆAB”ΎEΘ§DFΓΆBC”ΎFΘ§Ν§EFΘ°«σEFΒΡΉν–Γ÷ΒΘ°
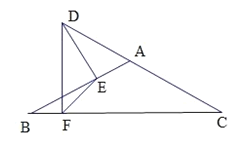
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ±±Ψ©ΒΎ“ΜΧθΒΊΧζœΏ¬Ζ”Ύ1971Ρξ1‘¬15»’’ΐ ΫΩΣΆ®‘Υ”ΣΘ°ΫΊ÷Ν2017Ρξ1‘¬Θ§±±Ψ©ΒΊΧζΙ≤ΓΑΫπ…Ϋ“χ…ΫΘ§≤Μ»γ¬ΧΥ°«ύ…ΫΓ±Θ°Ρ≥ –≤ΜΕœΆΤΫχΓΑ…≠Ν÷≥« –Γ±Ϋ®…ηΘ§Ϋώ¥Κ÷÷÷≤ΥΡάύ ςΟγΘ§‘ΑΝ÷≤ΩΟ≈¥”÷÷÷≤ΒΡ’β≈ζ ςΟγ÷–ΥφΜζ≥ι»ΓΝΥ4000ΩΟΘ§ΫΪΗςάύ ςΟγΒΡ÷÷÷≤ΩΟ ΐΜφ÷Τ≥……»–ΈΆ≥ΦΤΆΦΘ§ΫΪΗςάύ ςΟγΒΡ≥…ΜνΩΟ ΐΜφ÷Τ≥…Χθ–ΈΆ≥ΦΤΆΦΘ§Ψ≠Ά≥ΦΤΥ… ςΚΆ―ν ςΒΡ≥…Μν¬ ΫœΗΏΘ§«“―ν ςΒΡ≥…Μν¬ ΈΣ97%Θ§ΗυΨίΆΦ±μ÷–ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
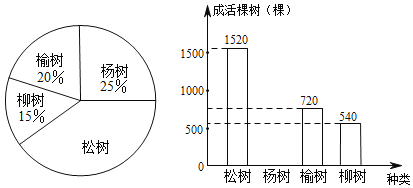
Θ®1Θ©…»–ΈΆ≥ΦΤΆΦ÷–Υ… ςΥυΕ‘ΒΡ‘≤–ΡΫ«ΈΣΓΓ ΓΓΕ»Θ§≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘ°
Θ®2Θ©ΗΟ –ΫώΡξΙ≤÷÷ ς16ΆρΩΟΘ§≥…ΜνΝΥ‘ΦΕύ…ΌΩΟΘΩ
Θ®3Θ©‘ΑΝ÷≤ΩΟ≈ΨωΕ®ΟςΡξ¥”’βΥΡάύ ςΟγ÷–―ΓΝΫάύ÷÷÷≤Θ§«κ”ΟΝ–±μΖ®Μρ ςΉ¥ΆΦ«σ«ΓΚΟ―ΓΒΫ≥…Μν¬ ΫœΗΏΒΡΝΫάύ ςΟγΒΡΗ≈¬ Θ°Θ®Υ… ςΓΔ―ν ςΓΔ”ή ςΓΔΝχ ςΖ÷±π”ΟAΘ§BΘ§CΘ§D±μ ΨΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
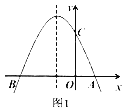
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§Εΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§Τδ÷–AΒψΉχ±ξΈΣ
ΒΡΆΦœσ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§Τδ÷–AΒψΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() Θ§Νμ≈ΉΈοœΏΨ≠ΙΐΒψ
Θ§Νμ≈ΉΈοœΏΨ≠ΙΐΒψ![]() Θ§MΈΣΥϋΒΡΕΞΒψΘ°
Θ§MΈΣΥϋΒΡΕΞΒψΘ°
![]() «σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
![]() «σ
«σ![]() ΒΡΟφΜΐ
ΒΡΟφΜΐ![]() Θ°
Θ°
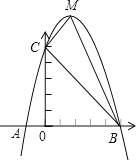
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
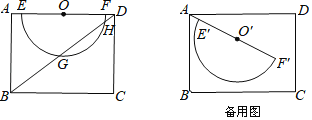
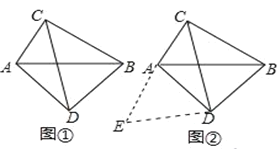
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§ABΘΫ6Θ§BCΘΫ8Θ§O «ADΒΡ÷–ΒψΘ§“‘OΈΣ‘≤–Ρ‘ΎADΒΡœ¬ΖΫΉςΑκΨΕΈΣ3ΒΡΑκ‘≤OΘ§ΫΜAD”ΎEΓΔFΘ°
ΥΦΩΦΘΚΝ§Ϋ”BDΘ§ΫΜΑκ‘≤O”ΎGΓΔHΘ§«σGHΒΡ≥ΛΘΜ
ΧΫΨΩΘΚΫΪœΏΕΈAFΝ§¥χΑκ‘≤O»ΤΒψAΥ≥ ±’κ–ΐΉΣΘ§ΒΟΒΫΑκ‘≤OΓδΘ§…ηΤδ÷±ΨΕΈΣE'FΓδΘ§–ΐΉΣΫ«ΈΣΠΝΘ®0ΘΦΠΝΘΦ180ΓψΘ©Θ°
Θ®1Θ©…ηFΓδΒΫADΒΡΨύάκΈΣmΘ§Β±mΘΨ![]() ±Θ§«σΠΝΒΡ»Γ÷ΒΖΕΈßΘΜ
±Θ§«σΠΝΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τΑκ‘≤OΓδ”κœΏΕΈABΓΔBCœύ«– ±Θ§…η«–ΒψΈΣRΘ§«σ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
Θ®sin49ΓψΘΫ![]() Θ§cos41ΓψΘΫ
Θ§cos41ΓψΘΫ![]() Θ§tan37ΓψΘΫ
Θ§tan37ΓψΘΫ![]() Θ§ΫαΙϊ±ΘΝτΠ–Θ©
Θ§ΫαΙϊ±ΘΝτΠ–Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§”κ
ΝΫΒψΘ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ°
Θ°

Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©‘ΎΗΟ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ «Ζώ¥φ‘ΎΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ΒΡ÷ή≥ΛΉν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψ
ΒΡ÷ή≥ΛΉν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ Χβ±≥ΨΑΘΚ
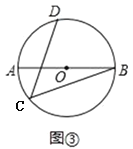
»γΆΦΔΌΘ§‘ΎΥΡ±Ώ–ΈADBC÷–Θ§ΓœACB=ΓœADB=90ΓψΘ§AD=BDΘ§ΧΫΨΩœΏΕΈACΘ§BCΘ§CD÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
–ΓΈβΆ§―ßΧΫΨΩ¥ΥΈ ΧβΒΡΥΦ¬Ζ «ΘΚΫΪΓςBCD»ΤΒψDΘ§Ρφ ±’κ–ΐΉΣ90ΓψΒΫΓςAED¥ΠΘ§ΒψBΘ§CΖ÷±π¬δ‘ΎΒψAΘ§E¥ΠΘ®»γΆΦΔΎΘ©Θ§“Ή÷ΛΒψCΘ§AΘ§E‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§≤Δ«“ΓςCDE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Υυ“‘CE=![]() CDΘ§¥”ΕχΒΟ≥ωΫα¬έΘΚAC+BC=
CDΘ§¥”ΕχΒΟ≥ωΫα¬έΘΚAC+BC=![]() CDΘ°
CDΘ°
ΦρΒΞ”Π”ΟΘΚ
Θ®1Θ©‘ΎΆΦΔΌ÷–Θ§»τAC=2Θ§BC=4Θ§‘ρCD= Θ°
Θ®2Θ©»γΆΦΔέΘ§AB «Γ―OΒΡ÷±ΨΕΘ§ΒψCΓΔD‘ΎΓ―…œΘ§ΜΓADΘΫΜΓBDΘ§»τAB=13Θ§BC=12Θ§«σCDΒΡ≥ΛΘ°
ΆΊ’ΙΙφ¬…ΘΚ
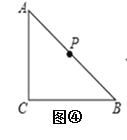
Θ®3Θ©»γΆΦ4,ΓςABC÷–Θ§ΓœACB=90ΓψΘ§AC=BCΘ§ΒψPΈΣABΒΡ÷–ΒψΘ§»τΒψE¬ζΉψAE=![]() ACΘ§CE=CAΘ§«“ΒψE‘Ύ÷±œΏACΒΡΉσ≤ύ ±Θ§ΒψQΈΣAEΒΡ÷–ΒψΘ§‘ρœΏΕΈPQ”κACΒΡ ΐΝΩΙΊœΒ « Θ°
ACΘ§CE=CAΘ§«“ΒψE‘Ύ÷±œΏACΒΡΉσ≤ύ ±Θ§ΒψQΈΣAEΒΡ÷–ΒψΘ§‘ρœΏΕΈPQ”κACΒΡ ΐΝΩΙΊœΒ « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com