Question

如图，四边形ABCD是菱形，对角线AC与BD交于点O，且AC=80，BD=60．动点M，N分别以每秒1个单位的速度从点A，D同时出发，分别沿A→O→D和D→A运动，当点N到达点A时，M，N同时停止运动．设运动时间为t秒．

（1）求菱形ABCD的周长．

（2）设△DMN的面积为S，求S关于t的解析式，并求S的最大值（提示：需分两种情况讨论）．

　

Answer 1

【考点】四边形综合题．

【分析】（1）根据勾股定理及菱形的性质，求出菱形的周长；

（2）在动点M、N运动过程中：①当0＜t≤40时，如答图1所示，②当40＜t≤50时，如答图2所示．分别求出S的关系式，然后利用二次函数的性质求出最大值．

【解答】解：（1）在菱形ABCD中，

∵四边形ABCD是菱形，对角线AC与BD交于点O，且AC=80，BD=60，

∴OA=40，OD=30，

∵AC⊥BD，

∴AD=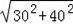=50．

∴菱形ABCD的周长为200．

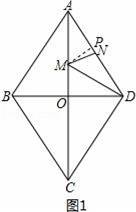
（2）过点M作MP⊥AD，垂足为点P．

①当0＜t≤40时，如图1，

∵，

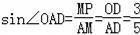
∴MP=AM•sin∠OAD=．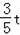

∴．

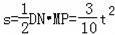
∵S随t的增大而增大，

∴当t=40时，最大值为480；

②当40＜t≤50时，如图2，

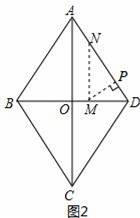
∴MD=80﹣t．

∵，

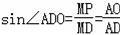
∴MP=．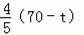

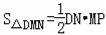
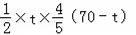
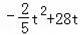
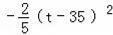
∴===+490．

∵S随t的增大而减小，

∴当t=40时，最大值为480．

综上所述，S的最大值为480．

【点评】本题考查了菱形的性质、勾股定理、解直角三角形、二次函数极值等知识点，涉及考点较多，有一定的难度．第（2）问中，动点M在线段AO和OD上运动时，是两种不同的情形，需要分类讨论；