
 ��ͼ����ƽ��ֱ������ϵ�У�����Ϊ��4��-1�����������߽�y����A�㣬��x����B��C���㣨��B�ڵ�C����ࣩ����֪A�������Ϊ��0��3����
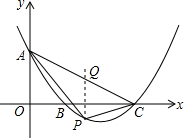
��ͼ����ƽ��ֱ������ϵ�У�����Ϊ��4��-1�����������߽�y����A�㣬��x����B��C���㣨��B�ڵ�C����ࣩ����֪A�������Ϊ��0��3�������� ��1����֪�����ߵĶ������꣬���ö���ʽ�������ߵĽ���ʽ��Ȼ��A������������У���������˶��κ����Ľ���ʽ��
��2���ٹ�P��y���ƽ���ߣ���AC��Q�������ֱ��AC�Ľ���ʽ�������P������꣬�����ɱ�ʾ��P��Q�������꣬Ҳ�͵ó���PQ�ij���Ȼ���������������ļ��㷽�����ɵó����ڡ�PAC�������P�������ĺ�����ϵʽ���������ú��������ʼ��������PAC������������Ӧ��P�����ꣻ
�ڵ���PAM�ǵ���ֱ��������ʱ����M��4��y����P��m��$\frac{1}{4}$m2-2m+3��������������������ۣ���M=90�㣬MA=MP����A=90�㣬AM=AP����P=90�㣬PA=PM��
��� �⣺��1����������Ϊy=a��x-4��2-1��
�������߾�����A��0��3����
��3=a��0-4��2-1��
���a=$\frac{1}{4}$��
�������ߵĽ���ʽΪy=$\frac{1}{4}$��x-4��2-1����y=$\frac{1}{4}$x2-2x+3�� ��2������ͼ������P��ƽ����y���ֱ�߽�AC�ڵ�Q��
��2������ͼ������P��ƽ����y���ֱ�߽�AC�ڵ�Q��
�����AC�Ľ���ʽΪy=-$\frac{1}{2}$x+3��
��P���������m��$\frac{1}{4}$m2-2m+3����
��Q���������m��-$\frac{1}{2}$m+3����
��PQ=-$\frac{1}{2}$m+3-��$\frac{1}{4}$m2-2m+3��=-$\frac{1}{4}$m2+$\frac{3}{2}$m��
��S��PAC=S��PAQ+S��PCQ=$\frac{1}{2}$����-$\frac{1}{4}$m2+$\frac{3}{2}$m����6
=-$\frac{3}{4}$��m-3��2+$\frac{27}{4}$��
�൱m=3ʱ����PAC��������Ϊ$\frac{27}{4}$��
��ʱ��P�������Ϊ��3��-$\frac{3}{4}$����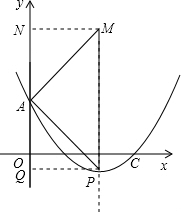 �ڡߵ�P����������λ��A��C����֮���һ�����㣬��P�ĺ�����Ϊm��C��6��0����
�ڡߵ�P����������λ��A��C����֮���һ�����㣬��P�ĺ�����Ϊm��C��6��0����
��0��m��6��
����PAM�ǵ���ֱ��������ʱ����M��4��y����P��m��$\frac{1}{4}$m2-2m+3���������������
�������M=90�㣬MA=MP����ȻM��4��3����P��4��-1����
�������A=90�㣬AM=AP����ͼ����MN��y���ڵ�N��PQ��y���ڵ�Q����֤��AMN�ա�PAQ��
��MN=AQ=4����3-��$\frac{1}{4}$m2-2m+3��=4�����m=4��
����P��4��-1����
��AN=PQ=4��
��y-3=4��
��y=7��
��M��4��7����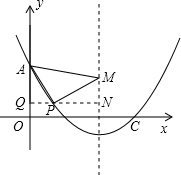 �������P=90�㣬PA=PM����ͼ����MN��y���ڵ�Q�����Գ����ڵ�N����֤��PQA�ա�MNP��
�������P=90�㣬PA=PM����ͼ����MN��y���ڵ�Q�����Գ����ڵ�N����֤��PQA�ա�MNP��
��PQ=MN��AQ=PN��
��m=y-��$\frac{1}{4}$m2-2m+3����3-��$\frac{1}{4}$m2-2m+3��=4-m��
��y=2m-1��
��AP=PM��
��m2+��$\frac{1}{4}$m2-2m+3-3��2=��m-4��2+��$\frac{1}{4}$m2-2m+3-2m+1��2��
������m3-14m2+40m-32=0��
��m-2����m2-12m+16��=0��
���m1=2��m2=6+2$\sqrt{5}$��m3=6-2$\sqrt{5}$��
��m1=2ʱ��y=3��M��4��3����P��2��0����AP2+PM2=13+13=26��AM2=16��m1=2����������ȥ��
m2=6+2$\sqrt{5}$��6������������ȥ��
��m3=6-2$\sqrt{5}$ʱ��M��4��11-4$\sqrt{5}$����P��6-2$\sqrt{5}$��5-2$\sqrt{5}$����AP2+PM2=80-32$\sqrt{5}$+80-32$\sqrt{5}$=160-64$\sqrt{5}$=AM2=160-64$\sqrt{5}$��m3=6-2$\sqrt{5}$�������⣮
�����������������ߵĶԳ����ϴ��ڵ�M��ʹ�á�PAM�ǵ���ֱ�������Σ���ʱ��M�������ǣ�4��3����4��7����M��4��11-4$\sqrt{5}$����
���� �����Ƕ��κ������ۺ����ͣ������漰�����ô���ϵ��������κ�����һ�κ����Ľ���ʽ�������ε����������ֱ�������ε����ʵ�֪ʶ���ۺ��Խ�ǿ����һ���Ѷȣ������йض�������ʱҪע����������������۽����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
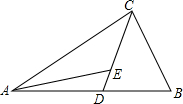 ��ͼ����ABC�У���D��AB���ϣ�AD=CD����E��CD�ϣ���ABC+��AEC=180�㣬ͼ���Ƿ������BC��ȵ��߶Σ������ڣ����ҳ���������֤�����������ڣ���˵�����ɣ�
��ͼ����ABC�У���D��AB���ϣ�AD=CD����E��CD�ϣ���ABC+��AEC=180�㣬ͼ���Ƿ������BC��ȵ��߶Σ������ڣ����ҳ���������֤�����������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
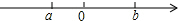 ��֪ʵ��a��b��������λ����ͼ��ʾ������$\sqrt{{a}^{2}}$+|a-b|=-2a+b��
��֪ʵ��a��b��������λ����ͼ��ʾ������$\sqrt{{a}^{2}}$+|a-b|=-2a+b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
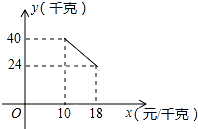 ij����������һ�ֲ�Ʒ�����ֲ�Ʒ�ijɱ���Ϊ10Ԫ/ǧ�ˣ���֪���ۼ۲����ڳɱ��ۣ�����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ�ˣ��г����鷢�֣��ò�Ʒÿ���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ�֮��ĺ�����ϵ��ͼ��ʾ��
ij����������һ�ֲ�Ʒ�����ֲ�Ʒ�ijɱ���Ϊ10Ԫ/ǧ�ˣ���֪���ۼ۲����ڳɱ��ۣ�����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ�ˣ��г����鷢�֣��ò�Ʒÿ���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ�֮��ĺ�����ϵ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com