
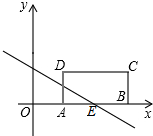
 如图所示,在平面直角坐标系中,矩形ABCD的边AB位于x轴,A(1,0),B(3,0),矩形的宽AD为1,一条直线y=kx+2(k≠0)与折线ABC交于点E.
如图所示,在平面直角坐标系中,矩形ABCD的边AB位于x轴,A(1,0),B(3,0),矩形的宽AD为1,一条直线y=kx+2(k≠0)与折线ABC交于点E.| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
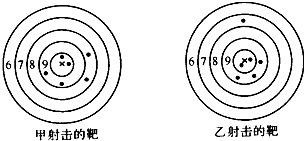 如图是甲,乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.
如图是甲,乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.查看答案和解析>>
科目:初中数学 来源: 题型:
| 里程(千米) | 票价(元) | |
| 甲→乙 | 20 | … |
| 甲→丙 | 16 | … |
| 甲→丁 | 10 | … |
| … | … | … |
| 出发时间 | 到达时间 | |
| 甲→乙 | 8:00 | 9:00 |
| 乙→甲 | 9:20 | 10:00 |
| 甲→乙 | 10:20 | 11:20 |
| … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com