【题目】如图，在平面直角坐标系中，点
、
分别在笫一、二象限，
轴于点
，连接
、
、
，且
（1）如图1，若
，
，
，探究
、
之间的数量关系，并证明你的结论
（2）如图2，若
，
，探究线段
、之间的数量关系，并证明你的结论．
科目：初中数学 来源： 题型：
【题目】如图，线段AB两端点坐标分别为A（﹣1，5）、B（3，3），线段CD两端点坐标分别为C（5，3）、D （3，﹣1）数学课外兴趣小组研究这两线段发现：其中一条线段绕着某点旋转一个角度可得到另一条线段，请写出旋转中心的坐标________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】郑州市自2019年12月1日起推行垃圾分类，广大市民对垃圾桶的需求剧增．为满足市场需求，某超市花了7900元购进大小不同的两种垃圾桶共800个，其中，大桶和小桶的进价及售价如表所示．
大桶 | 小桶 | |
进价（元/个） | 18 | 5 |
售价（元/个） | 20 | 8 |
（1）该超市购进大桶和小桶各多少个？
（2）当小桶售出了300个后，商家决定将剩下的小桶的售价降低1元销售，并把其中一定数量的小桶作为赠品，在顾客购买大桶时，买一赠一（买一个大桶送一个小桶），送完即止．
请问：超市要使这批垃圾桶售完后获得的利润为1550元，那么小桶作为赠品送出多少个？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB⊥BC，射线CM⊥BC，且BC=4，AB=1，点P是线段BC（不与点B、C重合）上的动点，过点P作DP⊥AP交射线CM于点D，连结AD．
(1)如图1，若BP=3，求△ABP的周长；
(2)如图2，若DP平分∠ADC，试猜测PB和PC的数量关系，并说明理由；
(3)若△PDC是等腰三角形，作点B关于AP的对称点B′，连结B′D，则B′D=_____．（请直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
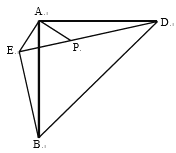
【题目】如图，
为边长不变的等腰直角三角形，
，
，在外取一点
，以
为直角顶点作等腰直角
，其中
在内部，
，
，当E、P、D三点共线时，
．
下列结论：
①E、P、D共线时，点
到直线
的距离为
；
②E、P、D共线时，
；
；
④作点
关于
的对称点
，在
绕点
旋转的过程中，
的最小值为
；
⑤绕点旋转,当点
落在
上，当点
落在
上时，取
上一点
，使得
，连接
，则
．
其中正确结论的序号是___．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A在双曲线y＝的第一象限的那一支上，AB垂直于x轴与点B，
点C在x轴正半轴上，且OC＝2AB，点E在线段AC上，且AE＝3EC，点D为OB的中点，若△ADE
的面积为3，则k的值为 ▲ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】仔细阅读下面例题，解答问题：
例题：已知二次三项式
有一个因式是
，求另一个因式以及
的值．
解：设另一个因式为
，得
，
则
，
，
解得，
，
∴另一个因式为
，的值为
．
仿照例题方法解答：
（1）若二次三项式
的一个因式为
，求另一个因式；
（2）若二次三项式
有一个因式是
，求另一个因式以及
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】两个工程队共同参与一项筑路工程，甲队单独施工3个月，这时增加了乙队，两队又共同工作了2个月，总工程全部完成，已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月，设甲队单独完成全部工程需
个月，则根据题意可列方程中错误的是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（ ）
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
