Question

15．正方形ABCD边长为1，P为BC边上一动点．
（1）如图1，当P为DC中点时，作BP的垂直平分线交边AD、BC于M、N，过PN，求tan∠PNC；
（2）如图2，过C作CQ∥BD交BP延长线于Q，若BD=BQ，求CQ的长；
（3）请直接写出$\frac{{P{A^2}}}{{P{B^2}}}$的最大值．

Answer 1

分析 （1）利用△EBN∽△CBP能够得出BN的值，再根据CN=BC-BN得出CN，利用正切的定义即可求出tan∠PNC的值；
（2）由△CPQ∽△DPB可得出两三角形各边的比例关系，设PC=a，结合相似比与BQ=BD得出a的值，再回归△CPQ∽△DPB中找到CQ的长；
（3）设PC=a，找出$\frac{P{A}^{2}}{P{B}^{2}}$=1+$\frac{1-2a}{1+{a}^{2}}$，由一次函数1-2a递减与二次函数1+a²单调递增，可得出$\frac{P{A}^{2}}{P{B}^{2}}$在0≤a≤1上单调递减，从而找出最大值．

解答 解：（1）令PB与MN的交点为点E，如图1．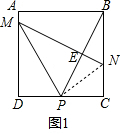

在Rt△BCP中，由勾股定理得：BP=$\sqrt{B{C}^{2}+C{P}^{2}}$，
∵正方形ABCD边长为1，P为DC中点，
∴CP=$\frac{1}{2}$，BP=$\frac{\sqrt{5}}{2}$．
∵MN为线段BP的垂直平分线，
∴BE=$\frac{1}{2}$PB=$\frac{\sqrt{5}}{4}$，∠BEN=90°，
∵∠BCP=90°，∠EBN=∠CBP，
∴△EBN∽△CBP，
∴$\frac{BN}{BP}$=$\frac{BE}{BC}$，∴BN=$\frac{5}{8}$．
∵CN=BC-BN=$\frac{3}{8}$，
∴tan∠PNC=$\frac{CP}{CN}$=$\frac{4}{3}$．
（2）依照题意画出图形，如图2．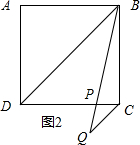

∵正方形ABCD边长为1，且BD=BQ，
∴BQ=BD=$\sqrt{2}$．
∵CQ∥BD，
∴∠CQP=∠DBP，∠QCP=∠BDP，
∴△CPQ∽△DPB，
∴$\frac{CQ}{DB}$=$\frac{QP}{BP}$=$\frac{CP}{DP}$．
令CP=a（0＜a＜1），则DP=1-a，
由勾股定理可知：BP=$\sqrt{1+{a}^{2}}$，
∴QP=BQ-BP=$\sqrt{2}$-$\sqrt{1+{a}^{2}}$．
∵$\frac{QP}{BP}$=$\frac{CP}{DP}$，即$\frac{a}{1-a}$=$\frac{\sqrt{2}-\sqrt{1+{a}^{2}}}{\sqrt{1+{a}^{2}}}$，
整理得a²-4a+1=0，
解得a=2-$\sqrt{3}$，或a=2+$\sqrt{3}$（舍去）．
∵$\frac{CQ}{DB}$=$\frac{CP}{DP}$，
∴CQ=$\frac{\sqrt{6}-\sqrt{2}}{2}$．
（3）设PC=a（0≤a≤1），则PD=1-a．
由勾股定理可得：PA²=AD²+PD²=1+（1-a）²，PB²=BC²+PC²=1+a²，
∴$\frac{P{A}^{2}}{P{B}^{2}}$=$\frac{1+（1-a）^{2}}{1+{a}^{2}}$=1+$\frac{1-2a}{1+{a}^{2}}$．
∵在0≤a≤1时，1-2a单调递减，1+a²单调递增，
即$\frac{P{A}^{2}}{P{B}^{2}}$=1+$\frac{1-2a}{1+{a}^{2}}$在0≤a≤1上单调递减，
故当a=0时，$\frac{P{A}^{2}}{P{B}^{2}}$取得最大值，最大值为1+$\frac{1-0}{1+0}$=2．

点评 本题考查了四边形综合运用、相似三角形的判定及性质、勾股定理以及函数的单调性，解题的关键是：（1）（2）利用相似三角形的判定及性质；（3）借助一次函数与二次函数的单调性求取极值．本题属于中等偏难题，失分点在（2）中相似三角形的各边长度不好断定，此处用到了勾股定理，解一元二次方程先求出PC的长，再回归相似三角形借助相似比得出结论．