
如图已知:直线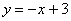 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线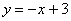 上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
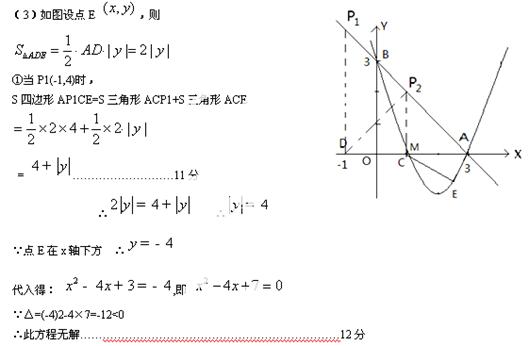
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.
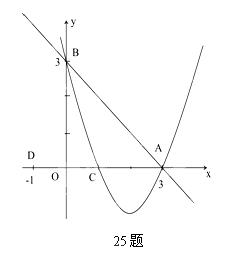
解(1):由题意得,A(3,0 ),B(0,3)
),B(0,3)
 ∵抛物线经过A、B、C三点,∴把A(3,0),B(0,3),C(1,0)三点分别代入
∵抛物线经过A、B、C三点,∴把A(3,0),B(0,3),C(1,0)三点分别代入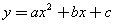 得方程组
得方程组
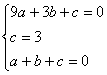 ……3分
……3分
解得: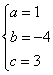
∴抛物线的解析式为 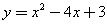 ………………5分
………………5分
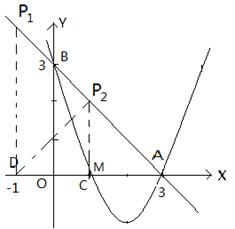
(2)由题意可得:△ABO为等腰三角形,如图所示,
若△ABO∽△AP1D,则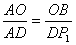
∴DP1=AD=4 ,
∴P1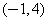 ……………………………………………… …………7分
……………………………………………… …………7分
若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4,
∵△ABO为等腰三角形, ∴△ADP2是等腰三角形,由三线合一可得:DM=AM=2= P2M,即点M与点C重合∴P2(1,2)……………………10分
 ②当P2(1,2)时,S四边形AP2CE=S三角形ACP2+S三角形ACE =
②当P2(1,2)时,S四边形AP2CE=S三角形ACP2+S三角形ACE = 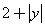
∴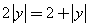 ∴
∴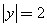
∵点E在x轴下方 ∴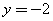 代入得:
代入得: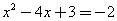
即 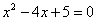 ,∵△=(-4)2-4×5=-4<
,∵△=(-4)2-4×5=-4< 0
0
∴此方程无解
综上所述,在x轴下方的抛物线上不存在这样的点E.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
如图 ,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=6 ,∠ABE=60°.
,∠ABE=60°.
①求AD的长; ②求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
⑴从中随机抽出一张牌,牌面数字是偶数的概率是__ ___________;
___________;
⑵从中随机抽出二张牌,两张牌牌面数字的和是5的概率是_____________;
⑶ 先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放
回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画
树状图或列表的方法求组成的两位数恰好是4的倍数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
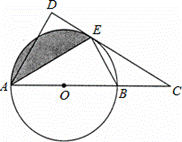
如图,⊙A、⊙B的半径分别为4、2,且AB=12.若作⊙C使得圆心在一直线AB上,且⊙C与⊙A外切,⊙C与⊙B相交于两点,则⊙C的半径可以是
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
我区有15所中学,其中九年级学生共有3000名.为了了解我区九年级学生的体重情况,请你运用所学的统计知识,将解决上述问题要经历的几个重要步骤进行排序.①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.则正确的排序为 .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
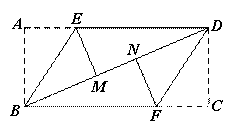
把一张矩形纸片,按如下图所示操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com